l'équation du temps

Quand les horlogers font mentir le soleil et ses cadrans solaires!

et quand le "jour le plus long" est en réalité le 22 décembre!

Il est vrai que selon Sénèque (-4/65):

"Horam non possum certam tibi dicere: facilius inter philosophos quam inter horologia conveniet".

Dans l’œuvre satirique l'"Apo-coloquint-ose" (pour parodie de apo-thé-ose!), Sénèque évoque ainsi l'heure de la mort violente de l'empereur Claude (-10/54) père adoptif de Néron (37-68), en égratignant les gnomonistes!

Mais les vraies raisons du mensonge du soleil viennent de la terre et de deux caractéristiques de son chemin dans l'espace: son orbite elliptique autour du soleil est parcourue selon la loi des aires et son axe de rotation n'est pas perpendiculaire au plan de l'orbite. C'est le cas de toutes les planètes d'ailleurs, même sûrement les exo...

Combien de critiques ont pu ainsi être faites, à tort, aux gnomonistes, avant Kepler et ses ellipses et avant le "Longitude Act" qui lance, en 1714, le défi du calcul de la longitude en mer. Ce défi, qui deviendra celui de l'extrême précision des horloges embarquées, sera relevé en plusieurs étapes, de 1749 à 1775, par l'anglais Harrison (1693-1776) avec la "H5", montre précise au tiers de seconde par jour.
Les philosophes n'ont pas fait autant de progrès dans leurs débats...

courbe en huit d'un soleil uniforme

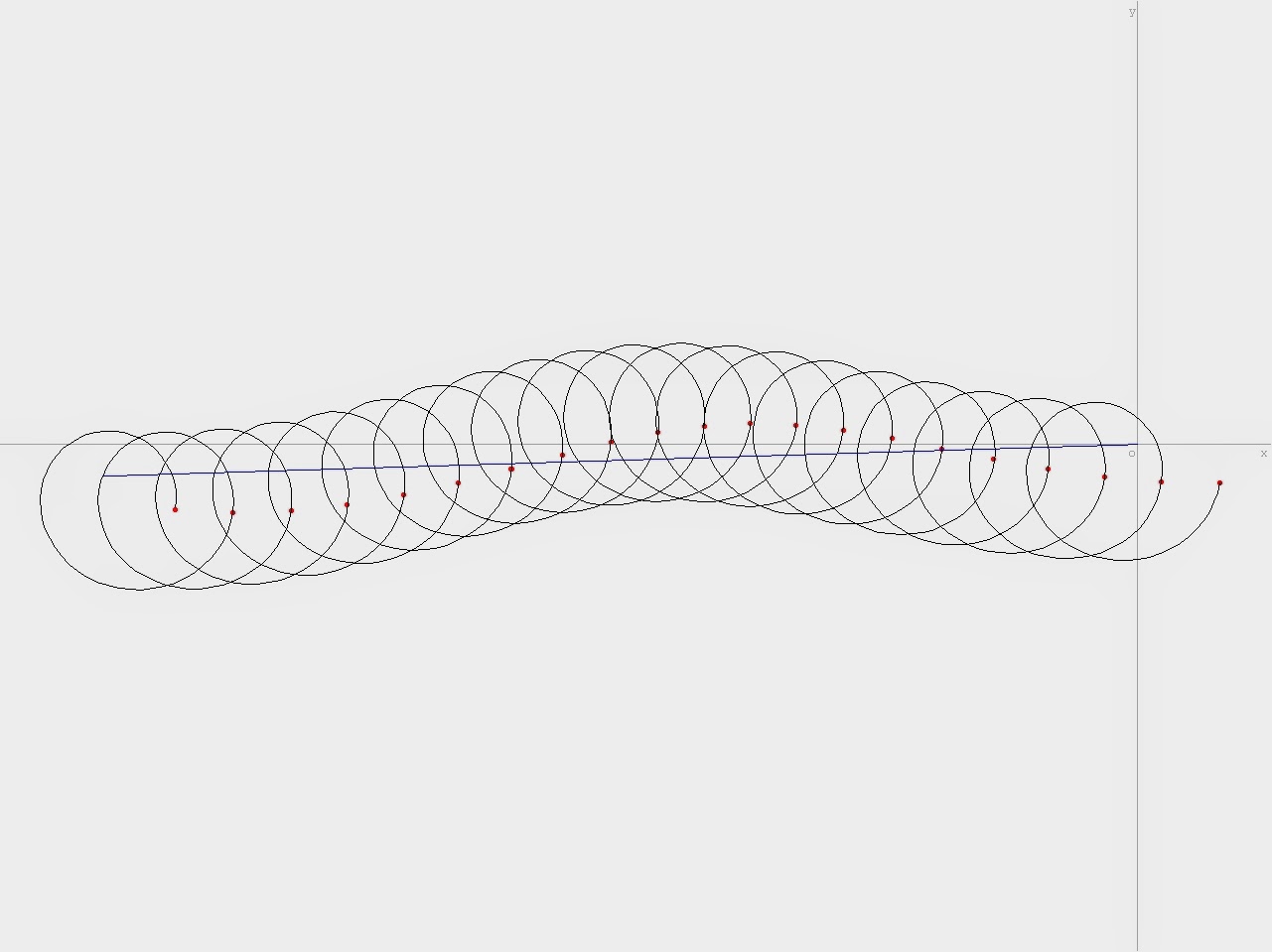
 L'écliptique, incliné sur le plan de l'équateur céleste, tourne autour de l'axe des pôles de la terre. Le soleil parcourt l'écliptique dans le sens inverse. Supposons d'abord que ces deux mouvements se fassent à vitesse uniforme. La trace du soleil à midi sur la sphère céleste sera alors une courbe en forme de huit gauche. L'ascension droite du soleil, c'est à dire l'arc dessiné en rouge, ne sera égal au temps, l'arc dessiné en bleu, que lors des passages aux équinoxes et aux solstices. L'écart s'appelle la "réduction à l'équateur", sa représentation est un trèfle à 4 feuilles, feuilles rouges pour un écart négatif, vertes pour un écart positif. Par une transformation conchoïdale, c'est à dire en augmentant le rayon polaire d'une quantité constante on peut donner au trèfle une apparence de haricot (!): c'est la courbe en rouge. La réduction à l'équateur est alors la différence entre courbe rouge et cercle noir.

l'hippopède d'Eudoxe de Cnide

 La courbe en forme de huit gauche est celle étudiée pour la première fois par l'astronome Eudoxe (-406/-355) à Cnide, ville de Grande Grèce célèbre pour l'Aphrodite de Praxitèle (-400/-320), elle est appelée hippopède car une entrave de cheval avait cette forme (voir à ce sujet l'excellent site mathcurve.com). C'est l'intersection d'une sphère et d'un cylindre qui lui est tangent ou d'une sphère et d'un cône dont l'axe lui est tangent. Elle a des propriétés étonnantes: ses projections sur les plans de symétrie sont un arc de parabole (en vert), un cercle et une affine de lemniscate de Gérono (1799-1891),en noir, sa projection stéréographique depuis le centre de la sphère est une affine de lemniscate de Bernoulli (1654-1705) en bleu. Pour une obliquité de pi/2 on a la courbe de Viviani (1622-1703) particulièrement extraordinaire...

conséquence de la loi des aires: rotation du huit

 
En réalité, la terre subit la loi des aires et le mouvement du soleil apparent n'est pas uniforme sur l’écliptique. Supposons que le périhélie coïncide avec l'origine du temps, alors l'ensemble de la courbe est déformée par une rotation, témoin de l'amplification symétrique des écarts. On met ainsi en évidence la deuxième composante de l'équation du temps appelée "équation du centre" (au moyen âge on désignait par le mot équation une différence de faible amplitude entre deux quantités). Le trèfle n'en est plus un: deux pétales sont hypertrophiées et deux hypotrophiées, mais elles restent symétriques, et le haricot est encore plus étranglé et de façon asymétrique.

l'équation du temps

Mais le périhélie ne coïncide pas avec le point gamma. Le décalage introduit une déformation supplémentaire: quand le soleil est au dessus de l'équateur, l'épaisseur de la boucle est réduite alors qu'elle est amplifiée lorsque le soleil est au dessous. Les quatre pétales du trèfle sont inégales et le haricot "accuse le coup".

l'équation du temps comme l'aiment les horlogers

La courbe rouge dessinée depuis le début n'est autre que la came qu'utilisent les constructeurs de montres pour mouvoir l'aiguille qui donne l'équation du temps, comme l'indique le cadran du haut à droite.
L'équation (au sens moderne) de la réduction à l'équateur est: r = arctan(cos(oblicité)xtan(t))-t. Celle de l'équation du centre est transcendante. Si on limite chacune de ces deux équations au premier terme de leur développement limité, les courbes algébriques donnent des courbes connues: le quadrifolium et le limaçon d'Etienne Pascal (1588-1651). Durant le processus croissant de transformation conchoïdale, le limaçon passe par la cardioïde et le quadrifolium  par le double oeuf de Clairaut (1713-1765). Ces courbes apparaissent sous le cadran.
Les intersections de la courbe rouge de l'équation du temps avec le cercle en pointillé noir donnent les 4 jours de l'année pour lesquels le soleil est en concordance avec l'horloge (équation nulle).
La courbe en jaune foncé donne l'écart entre 24h et le temps mis par le soleil pour revenir le lendemain à midi: c'est la vraie durée du jour. Cette information, contrairement à l'équation du temps qui ne peut que difficilement être appréhendée, serait facilement contrôlable par le propriétaire d'une montre qui la présenterait, comme ici en jaune foncé sur le cadran du haut.
C'est l'importance et le signe de cet écart qui règle la variation de l'équation du temps. Les intersections de cette courbe avec le cercle en pointillé noir donnent les 4 jours de l'année pour lesquels le soleil "tourne" en exactement 24h. Ces jours sont des maxima et minima pour l'équation du temps.

équation, ses composantes, durée du jour

La courbe en rouge donne les valeurs de l'équation du temps et les dates qui caractérisent son évolution. Au milieu de la figure, en bleu l'incidence de la réduction à l'équateur dont la période est de 6 mois et en gris celle de l'équation du centre de période annuelle. En bas l'écart entre la durée réelle du jour et la moyenne de 24h00m00s et ses 2 composantes.
L'effet saisonnier de l'obliquité de l'écliptique est largement prépondérant par rapport à celui de la loi des aires. Cette loi, qui retrace la vitesse de la terre autour du soleil, ne fait qu'amplifier d'un tiers la paresse d'Apollon au solstice d'hiver et la diminuer dans la même proportion au solstice d'été, elle est sans effet notable aux équinoxes.

analemme et croisant

 Autres représentations, en huit, de l'équation du temps , l'analemme, et de la durée du jour, en croissant.
Le jour du printemps, le soleil est en retard de 17.7 m et ce retard diminue jusqu'à s'annuler le 15/04: ce jour là le soleil est à l'heure: le cadran solaire est juste. Mais ensuite l'astre du jour prend de l'avance, cette avance passe par un maximum de 3.6 m le 14/05: alors la durée du jour est de 24h exactement.
L'avance diminue ensuite jusqu'à s'annuler le 13/06: le soleil est à nouveau à l'heure mais dès le lendemain il prend du retard, un retard qui croît jusqu'à un maximum de 6.4 m atteint le 26/07, jour de durée égale à 24h exactement.
Ce retard se réduit alors et s'annule le 1/09, troisième jour pour lequel le cadran solaire est juste. Jusqu'à Noël,  le soleil va alors être en avance, cette avance passant par un maximum absolu de 16.4m le 3/11. Ce jour là, qui dure exactement 24h, à midi local à Sion le soleil est déjà 4.5° à l'est du méridien plein sud! L'avance du soleil diminue ensuite car les jours rallongent de plus en plus depuis le 17/09 jour le plus court de l'année (23h59m38.6 s) : le 22 décembre est le jour le plus long de l'année: 24h00m29.8s.
Le 25 décembre le soleil est à l'heure pour la quatrième et dernière fois de l'année. Jusqu'au printemps il sera en retard avec un maximum de 14.2 m le 14/02, quatrième et dernière date pour laquelle la durée du jour est 86400 s.

heures légale et naturelle proches

matinées raccourcies

repas très tardifs

La loi des aires induit une modification des dates pour lesquelles ont lieu les levers de soleil les plus matinaux et les couchers les plus tardifs: elles ne correspondent plus aux solstices.
C'est ainsi que le lever de soleil le plus matinal a lieu le 15 juin et le plus tardif le 1er janvier. 
Le coucher de soleil le plus tardif a lieu le 26 juin et le moins tardif le 11 décembre.
Les courbes des figures ci-dessus donnent l'heure légale des levers et couchers dans 3 villes européennes.
L'Europe connaît une heure légale identique depuis la Serbie jusqu'à l'Espagne alors que l'écart de longitude dépasse 30°, soit 2 heures. Ceci a pour conséquence un décalage important dans le rythme de vie des nationaux, décalage accentué en été avec le changement d'heure depuis le dernier dimanche de mars jusqu'au dernier dimanche d'octobre. Ainsi, le 26 juin, la matinée, jusqu'à midi, ne dure que la moitié de l'après-midi à Saint Jacques de Compostelle, alors qu'à Belgrade l'écart entre matinée et après-midi n'est que d'un peu plus d'une heure.
Le pèlerin serbe devra adapter son horloge biologique au cours de son pèlerinage!

La planète mars ressemble beaucoup à la terre dans certaines de ses caractéristiques orbitales: l'obliquité est de 25.2° (23.4° pour la terre), sa rotation dure 24.623 h (on appelle le jour martien: "sol"). Mars étant plus éloignée du soleil, l'année dure 686.96 jours terrestres soit 668.58 sols (sur mars, une année sur deux est bissextile!).
L'effet de la réduction à l'équateur est donc analogue à ce qui se passe sur la terre.
Le périhélie de l'orbite, par rapport au point gamma martien, se trouve, comme sur la terre, au voisinage du solstice d'hiver. Par contre, l'excentricité est plus de 5 fois plus forte: 0.0934 pour 0.0167. L'effet de l'équation du centre est donc considérable.
En conséquence l'analemme de mars ne présente pas une forme en huit: l'équation du centre déforme le huit de la réduction à l'équateur à tel point qu'il en résulte une courbe convexe.
La came des horlogers martiens ne présente qu'un seul creux. Les maxima de l'équation du temps sont +51 m de sol et -40 m de sol et les durées du sol vont de -22 s de sol à +41 s de sol.
Pour une certaine position du périhélie, l'analemme présente une forme intermédiaire avec un point de rebroussement. Pour la terre cela ne se produirait que pour une excentricité de 0.049.
Une autre conséquence de la forte excentricité et de la position du périhélie concerne la durée des saisons. Les saisons chaudes dans l'hémisphère nord durent 56% de l'année: printemps 193 sols (29%) et l'été 179 sols (27%). La température sur mars cependant n'est jamais positive!

la came des horlogers martiens

l'analemme de mars en 2014 et en ? BC

la Voie Lactée

"Cette large et ample route, dont la poussière est d'or et le pavement, les étoiles;
ainsi les étoiles t'apparaissent, vues dans la Galaxie,
cette Voie Lactée, qui, de nuit, t'entoure telle une ceinture poudrée d'étoiles".

C'est ainsi que John Milton (1608-1674) - cité par Thomas Wright (1711-1786) in "Textes essentiels", anthologie de Jean Pierre Verdet, Larousse 1993 - décrit la grande arche de matière lumineuse qui parcourt le ciel nocturne, reposant sur deux points opposés de l'horizon.
Il y a dans ce spectacle de quoi s'interroger. 
Dans la mythologie grecque le ruban laiteux provient d'une giclée du lait maternel de Héra, lors de l'allaitement plus ou moins consenti d’Héraclès, fils illégitime de Zeus son époux et d'Alcmène épouse d’Amphitryon fils du roi de Tirynthe. Le mot grec pour lait est gala, galaktos au génitif, d'où "tou galaktos kyklos" pour cercle de lait.
Le poème de Manilius datant du début du premier siècle - cité par les mêmes - explique: "les  âmes valeureuses, libérées des soucis du corps, se rendent là et y mènent une vie éthérée". S'agit-il du Paradis?
Certains astronomes anciens imaginaient déjà que cette rivière de lait pouvait résulter d'une accumulation de petites étoiles. C'est la lunette de Galilée qui permit de le vérifier en1609.
Wright en 1750 émit la bonne hypothèse en estimant que ce grand cercle pouvait résulter de la vision qu'on aurait, depuis l'intérieur et par la tranche , d'une galette où un grand nombre d'étoiles seraient rassemblées.
Mais le concept de galaxie n'a pas cent ans: ce n'est qu'en 1930 que la communauté scientifique se met d'accord sur l'organisation de l'univers en galaxies.
Après Kepler et Galilée une nouvelle astronomie se met en place grâce aux progrès conjugués faits dans la mesure du temps, les outils mathématiques et les moyens d'observation: horloge à pendule, garde-temps, logarithmes, analyse, calculs différentiel et intégral, lunettes et télescopes géants...
Les jalons de cette évolution ont pour noms: Néper, Huygens, Cassini, Newton, Leibniz, d’Alembert, Halley, Bradley, Herschel, Euler, Lagrange, Laplace...
En deux siècles le système solaire, augmenté de l'anneau des astéroïdes entre mars et jupiter (dont les troyens positionnés aux points de Lagrange de l'orbite de jupiter), de la ceinture de Kuiper et du nuage d'Oort d'où viennent les comètes, est arpenté aux sens propre et figuré et on peut passer à l'étape suivante: les étoiles.

18/10/2014, 20h42 heure de Sion, la Voie Lactée (en rouge) est perpendiculaire à l'horizon, le centre de la galaxie est à l'horizon dans le Sagittaire, Deneb est au zénith, mars va se coucher.

Pour comprendre le ciel il est essentiel de connaître la distance des étoiles: l'astrométrie est la fondation des autres disciplines de l'astronomie.
Dès 1725 Bradley (1693/1762) s'était attelé au problème de la parallaxe annuelle, c'est à dire à la mise en évidence de l'écart d'angle présenté, en raison du déplacement de la terre sur son orbite, par une étoile observée à une certaine date et six mois après. Il avait choisi l'étoile Eltanin, la tête du dragon, malheureusement beaucoup trop loin, à 148 a.l. Une telle distance ne lui permettait pas de réussir avec les moyens encore peu performants dont il disposait, mais il a découvert que l'étoile décrivait une ellipse inattendue, explicable si on considérait que la vision des étoiles, comme celle du soleil, était affectée du phénomène optique de l'aberration dû à la transmission non instantanée de la lumière. Continuant ses observations et les débarrassant de l'effet de la précession, il découvre ensuite une oscillation de la déclinaison de l'étoile avec la même périodicité que la rétrogradation des nœuds lunaires (18.6ans), il appela ce phénomène la nutation. Les mathématiciens démontreront plus tard que précession et nutation découlent de la gravitation universelle.

observation d'Eltanin sur 20 ans, en bleu l'effet de la précession, en rouge celui de la nutation, les boucles annuelles résultent de l'aberration

La première parallaxe annuelle a été établie par l'astronome allemand Bessel (1787/1846) en 1838 pour l'étoile 61 Cygni de magnitude 5.2 qui se trouve à 11 a.l. seulement, soit une parallaxe égale à 0.35 seconde d'arc. Il lui fallut 286 mesures échelonnées sur 2 ans! (Danloux-Dumesnils, 1985). Les astronomes utilisent comme unité de distance pour les étoiles, le parsec, égal à l'inverse de la parallaxe exprimée en seconde d'arc: 61 Cygni est à 2.86 parsec (et Sirius à 2.67).
Au delà de 40 pc (130 a.l.) la méthode n'est plus applicable car la mesure précise de l'angle devient impossible. 300 étoiles seulement sont redevables de ce procédé exact à 10% près.
Dans l'attente de l'ère des satellites astrométriques de l'ESA (Hipparcos en 1989 et Gaia en 2013), on quitte alors le domaine du calcul pour procéder par analogie.
En 1784, Goodricke (1764/1786), astronome amateur, découvre la variabilité de l'étoile delta Céphée. Cette étoile passe très régulièrement de la magnitude 3.5 à 4.4 en 5.4 jours. En 1912 Miss Leavitt (1868/1921) découvre que ce type d'étoiles pulsantes est largement présent dans les nuages de Magellan, nébuleuses de l'hémisphère sud, et remarque que pour ces variables il y a proportionnalité entre la période et la luminosité. La magnitude visuelle étant fonction de la distance de l'étoile, il y a là une méthode pour apprécier cette distance. Reste à calibrer cette relation. Cela fut fait l'année suivante par l'astronome hollandais Hertzsprung (1873/1967)  par la méthode peu fiable de la "parallaxe statistique". En 1918 l'estimation doit être multipliée par 10, puis encore par 2 en 1952!
On utilise aussi les étoiles vibrantes du type RR Lyrae dont la magnitude absolue est très voisine de -0.6 et la période proche de quelques heures.
D'autres méthodes de plus en plus sophistiquées sont mises au point et, heureusement, convergent, ce qui atteste de leur pertinence.
Parallèlement l'image de la Galaxie prend forme dans l'imaginaire des astronomes: la densité variable d'étoiles dit que c'est une galette, la répartition des amas globulaires, hors de cette galette, amène à penser que le soleil n'est pas en son centre...
On aboutit à un disque renflé en son centre, d'un diamètre de 30.000 pc, d'une épaisseur de 3.000 pc avec une structure spiralée, le soleil à 8.000 pc du centre fait un tour complet en 230 millions d'années . Le plan de l'écliptique fait un angle de 63° avec le plan galactique.
La Galaxie comprend certainement une centaine de milliards d'étoiles 

M31 galaxie d'Andromède photo F.Borle observatoire de la SAVAR 09/2013

Son modèle est la nébuleuse de la constellation d'Andromède située à 700.000 pc (2.2 millions d'années lumière), seul objet visible à l’œil nu qui n’appartienne pas à notre Galaxie. En 1923 l'astronome américain Hubble (1889/1953) par l'analyse d'une céphéide qui y avait été détectée pouvait conclure à une distance d'un million d'années lumière.
La Voie Lactée appartient à l'amas de galaxies dénommé amas local qui n'est que l'un des très nombreux amas de galaxies existants...

Manilius, cité par les mêmes:
"L'étonnement doit vraiment atteindre leurs sens, de voir la large blessure du monde et la brèche éternelle du ciel".

Télescope Hubble crédit NASA, ESA

Ou bien Jean Rostand (1894-1977),  l'Homme 1940:
"Atome dérisoire, perdu dans le cosmos inerte et démesuré, il (l'Homme) sait que sa fiévreuse activité n'est qu'un petit phénomène local, éphémère, sans signification et sans but. Il sait que ses valeurs ne valent que pour lui et que, du point de vue sidéral, la chute d'un empire, ou même la ruine d'un idéal, ne compte pas plus que l'effondrement d'une fourmilière sous le pied d'un passant distrait.
Aussi n'aura-t-il d'autre ressource que de s'appliquer à oublier l'immensité brute qui l'écrase et qui l'ignore. Repoussant le stérile vertige de l'infini, sourd au silence effrayant des espaces, il s'efforcera de devenir aussi incosmique que l'univers est inhumain; farouchement replié sur lui-même, il se consacrera humblement, terrestrement, à la réalisation de ses desseins chétifs, où il feindra de prêter le même sérieux que s'ils visaient à des fins éternelles".

jupiter et ses satellites galiléens

Galilée (1564-1642), dès 1609 a eu, le premier, l'idée de tourner vers le ciel nocturne l'une de ces lunettes d'approche qui commençaient à circuler et étaient considérées comme une sorte de jeu, un gadget avant l'heure. Il a ainsi lancé l'observation instrumentale et a fait une moisson extraordinaire.
La lunette initiale avec un oculaire constitué d'une lentille divergente donnait une image droite mais ne permettait pas un grossissement important. Kepler, dont l'expertise en matière d'optique était reconnue, sut la modifier. Il remplaça l'oculaire divergent par une lentille convergente: le grossissement devenait important... mais l'image était renversée. La lunette était devenue un instrument scientifique.
Galilée découvre les gardes du corps de jupiter, les oreilles de saturne, les cornes de vénus, les montagnes de la lune, les taches sur le soleil, la nature de la voie lactée...

Les gardes du corps de jupiter sont vite transformés en conquêtes du roi des dieux: Io, Europe, Ganymède (le plus beau des mortels!) et Callisto.

17 mai 2014 22h UT Jupiter et les satellites galiléens vus de la terre

17 mai 2014 22h UT les mêmes "du point de vue de Sirius"

Le 17 mai 2014 vers 22UT, vu depuis la terre, Io passe sur le disque de jupiter (petit disque clair) et en même temps projette son ombre un peu à gauche. Callisto projette aussi son ombre mais un peu plus bas en raison de l'angle que fait le plan équatorial du système jovien avec l'écliptique.
Depuis juillet 2013, et pour 3 ans encore, Callisto, vu de la terre, passe sur le disque de jupiter et dans son ombre à chaque révolution. A partir de juillet 2016, son éloignement de la planète, l'inclinaison du plan équatorial et la position relative de la terre et de jupiter le feront échapper à ces phénomènes car il passera au dessus ou au dessous. Ensuite ces phénomènes vont reprendre.

18 mai 2014 17hUT Europe est occulté, Io va l'être

18 mai 2014 20hUT Europe, Io et Ganymède en quadrature

On peut parler de système jovien comme on parle de système solaire. Parmi les satellites galiléens les trois premiers présentent des caractéristiques extraordinaires. La période de Io est le double de celle d'Europe qui est elle-même le double de celle de Ganymède. D'après la troisième loi de Kepler, le cube du demi grand axe est proportionnel au carré de la période. Il en résulte que le cube du demi grand axe d'Europe vaut 4 fois celui de Io. La racine cubique de 4 étant 1.5874, la séquence 4, 2, 1 pour les périodes conduit à la séquence 1, 1.59, 2.53 pour les grands axes.

De plus, ces trois corps sont en résonance et leurs longitudes jovicentriques satisfont à la relation suivante: la somme de l'écart de longitude entre Io et Europe et du double de l'écart entre Ganymède et Europe est toujours égale à 180°. C'est ainsi que le 18 mai 2014, lorsque Io et Europe sont en conjonction, Ganymède est à la quadrature.

Laplace (1749-1827) a démontré que cette résonance est un état stable.

La masse propre d'un satellite n'intervient que très peu dans son mouvement autour d'un centre très massif. Mais entre les trois premiers satellites de jupiter les perturbations réciproques sont considérables car leur masses sont du même ordre de grandeur: la séquence est 1, 0.54, 1.68.

Le rapport de la masse au grand axe donne la séquence 1, 0.34, 0.66 ce qui signifie que l'énergie potentielle de Io est égale à la somme des énergies potentielles de ses 2 collègues réparties elles-mêmes en un tiers, deux tiers.

Cette organisation de 3 mobiles soumis à la gravitation autour d'un centre ne peut relever du hasard. Tient-elle à la proximité des orbites, à la puissance de l'attraction de jupiter...Pourquoi Callisto n'est-est-il pas concerné par ce phénomène?

Kepler a recherché éperdument, jusque dans les règles de l'harmonie musicale, la clef de l'organisation du système solaire. Qu'aurait-il pensé du système jovien?

La troisième loi de Kepler a été précisée et généralisée par Newton (1643-1727) qui a montré que le coefficient de proportionnalité entre cube du demi grand axe et carré de la période était un multiple des masses additionnées des deux corps.

Avec jupiter on dispose donc d'un ensemble à deux étages: la planète gravite autour du soleil et les galiléens autour de la planète. Ceci permet de calculer la masse de jupiter en fonction de celle du soleil puisque sa valeur figure dans deux relations indépendantes (à la masse près du galiléen qui, relativement, est très faible). On trouve que la masse du soleil vaut 1047 fois celle de jupiter. En appliquant cette méthode au satellite synchrone de la terre (géostationnaire) on trouve que la masse du soleil vaut 332.900 fois celle de la terre.

La masse de jupiter est donc 318 fois celle de la terre et son attraction sur ses satellites 318 fois plus forte. C'est ce qui explique que Io situé à peu près aussi loin du centre de jupiter, 421.000 km, que la lune ne l'est du centre de la terre, 384.000 km, tourne bien plus vite: 1.77 jours au lieu de 27.3 jours, soit 15 fois plus vite. Si la masse de la lune était négligeable par rapport à celle de la terre et si les demi grands axes étaient vraiment égaux la proportion calculée selon la loi de la gravitation serait égale à la racine carrée de 318 soit 17.8.

Io et Europe sont tellement rapides sur leurs orbites que leurs trajectoires rapportées au système solaire présentent une boucle pour Io et un point de rebroussement pour Europe. La trajectoire de Ganymède est plus classique mais encore très éloignée de celle de la lune qui, elle, est toujours concave vers le soleil.

trajectoires héliocentriques de Io, Europe, Ganymède (soleil vers le haut)

 2/3 de tour pour Io, 1/3 pour Europe, 1/6 pour Ganymède en conjonction

1 tour pour Io, 1/2 pour Europe en conjonction, 1/4 pour Ganymède

4/3 tour pour Io, 2/3 pour Europe, 1/3 pour Ganymède en conjonction

2 tours pour Io, 1 pour Europe, 1/2 pour Ganymède en conjonction

4 tours pour Io, 2 pour Europe, 1 pour Ganymède: retour à la case départ

Lorsque Io et Ganymède sont en opposition ou en conjonction, Europe précède ou suit Io de 60°.

Galilée a eu rapidement l'idée d'utiliser les éphémérides de ses satellites, notamment leurs éclipses et occultations, pour résoudre le "problème de la longitude" car il y avait bien là une horloge sans faille permettant de calculer l'écart de temps avec le midi local.  La méthode fut appliquée avec succès sur terre, mais pas depuis le pont d'un navire où elle restait hasardeuse, et elle a notamment permis aux savants et ingénieurs de l'Académie Royale des Sciences ,fondée en 1666 par Colbert (1619-1683), d'établir les bases de la future carte de France dite carte de Cassini.

C'est en 1676, en contrôlant les éphémérides calculés par J.D. Cassini (1625-1712), que l'astronome danois Ole Roemer (1644-1710) mit en évidence un décalage systématique entre les tables qui prenaient pour hypothèse une parfaite régularité et certaines observations. Il remarqua qu'aux environs de l'opposition de Jupiter, les éclipses des satellites se produisaient avec une avance d'une dizaine de minutes sur les tables alors qu'aux environs de la conjonction, elles étaient en retard de la même durée. Il eut l'idée d'imputer ces décalages au temps mis par la lumière pour franchir le différentiel de la distance terre-jupiter entre opposition et conjonction. Le calcul donne: 2 UA en 20 minutes, soit 300 millions de km en 1200 secondes, soit 250.000 km/s.
Le véritable décalage est égal à 16.6 minutes, ce qui met le soleil à 8.33 minute-lumière de la terre.

1693: des satellites de jupiter à la carte de France (source gallica-wikipédia)

les huit planètes du système solaire

Le système solaire est presque parfaitement plat, comme la voie lactée et comme les autres galaxies: c'est une constante de l'univers. Aux 5 astres errants connus depuis l'Antiquité il faut ajouter 2 planètes inventées aux 18ème et 19ème siècles. Uranus, père de Saturne et grand-père de Jupiter, jusqu'alors simple étoile, est reconnu en 1781 par William Herschel (1738-1822) observant au télescope de plus de 2m de focale qu'il s'était construit, d'abord comme nébuleuse parce qu'il a un diamètre apparent, puis comme comète parce qu'il bouge, et enfin en 1783 comme planète.
Les progrès de la mécanique céleste permettent dans les années 1820 de constater qu'uranus n'obéit pas rigoureusement aux lois de la gravitation et qu'il doit exister une troublante d'uranus.
Les mathématiciens anglais et français, dans une grande cacophonie, conduisent l'astronome allemand Galle (1812-1910) à observer en septembre 1846 à Berlin pour la première fois un astre qui bouge situé très près de la position calculée et communiquée par Le Verrier (1811-1877): c'est neptune. Neptune est un frère de Jupiter...

les huit planètes

Les pointillés des orbites d'uranus et neptune correspondent à la distance parcourue en un an.

les cinq planètes anciennes et la terre

Les pointillés des orbites de saturne et jupiter correspondent à la distance parcourue en un mois.

Les parties des orbites des planètes situées au dessus de l'écliptique: la terre n'est pas dans la moyenne du système solaire pour ce qui est de l'inclinaison.
Les longitudes du nœud ascendant des planètes  ne s'écartent pas de plus de 66° les unes des autres. Les nœuds se resserrent et tournent dans le sens direct d'environ 1° par siècle.

 

les  quatre planètes telluriques

Les pointillés des orbites correspondent à la distance parcourue en un jour.
mars et mercure bénéficient d'une assez forte excentricité, plus forte que celle de la terre, seule vénus tourne plus rond que la terre!

le jour du printemps 2014

Les vitesses linéaires sont inversement proportionnelles à la racine carrée du grand-axe, elles varient donc dans la proportion de 1 à 9 entre mercure et neptune, alors que les vitesses angulaires sont inversement proportionnelles à la racine carrée du cube du grand axe, elles varient donc dans la proportion de 1 à 700.
La rotation de la terre sur elle-même engendre un renflement équatorial que le soleil s'emploie à ramener dans le plan de l'écliptique. La lune l'y aide. Mais la rotation terrestre représente une énergie considérable, acquise lors de sa formation et le seul effet de ces efforts luni-solaires est celui constaté sur un gyroscope: l'axe de la rotation terrestre est pris dans une lente rotation autour de la direction perpendiculaire aux forces appliquées. Il en résulte que le jour du printemps est emporté lui-même dans cette rotation et qu'il précède chaque année la position qu'il avait l'année précédente d'une valeur de 50". Il entraîne avec lui le point gamma et toutes les coordonnées qui lui sont raccordées. Ce phénomène de la précession des équinoxes a été détecté par Hipparque (-190/-120) par l'analyse de relevés de positions d'étoiles vieux de plus d'un siècle.
Le pôle nord subit donc une rotation en quelques 26.000 ans autour du pôle de l'écliptique, seul point fixe à cette échelle, qui se trouve dans la constellation du Dragon, près de la nébuleuse NGC 6543, appelée l'œil de chat. Cette nébuleuse est formée par une étoile, semblable au soleil mais avec quelques milliards d'années en plus, qui vit ses derniers milliers d'années en projetant au loin ses couches supérieures, avalant au passage ses planètes...

foyers, grands-axes, oppositions de mars

Le soleil est un foyer commun aux ellipses décrites par les planètes. Les grands-axes sont distribués sans ordre apparent et les seconds foyers, notés ici "fi", restent intérieurs à l'orbite de mars (sauf uranus, de peu) et ne s'écartent pas sensiblement de l'écliptique.
Les pointillés des orbites correspondent à la distance parcourue en un jour.
Vénus, plus proche voisine de la terre, lui ressemble par la taille mais son atmosphère 100 fois plus épaisse, sa température de 400°, sa rotation très lente (et rétrograde, vénus aurait pu basculer...) entraînant que la journée dure 116 jours terrestres en font un enfer! Les vénusiens sont-ils responsables de l'effet de serre qui semble en être la cause? Exemple à méditer par les terriens?
La forte excentricité de l'orbite de mars fait que la planète est la plus facile à observer lors d'une opposition estivale. A l'opposition, les distances varient dans le rapport de 1 à 1.8 et celle de fin août 2003 a été exceptionnelle car elle s'est produite très près du périhélie de la planète. Il faut attendre fin juillet 2018 pour une fenêtre presque aussi favorable. En raison des vitesses variables de la terre et surtout de mars la succession des oppositions est irrégulière et varie de 764 jours (2010-2012) à 802 jours (2003-2005). Mars est la planète la plus attirante pour l'homme: obliquité et rotation proches des valeurs terrestres, présence d’atmosphère, de vents, de calottes de glace (carbonique...)...
La planète a déjà reçu la visite de nombreuses machines.
Pour atteindre mars en dépensant le moins d'énergie possible il faut embarquer dans un vaisseau qui n'est autre qu'une planète artificielle. Ce vaisseau va décrire une demi-orbite autour du soleil utilisant ainsi l'énergie de la gravitation. Au départ il quitte la terre en allant plus vite qu'elle puis il s'écarte du soleil et sa vitesse diminuant il se rapproche de l'orbite de mars. L'objectif se trouve derrière lui et va moins vite que lui. Le vaisseau ralentit encore et mars l'accoste.
Le périhélie de cette orbite est la position de la terre au moment du départ et son aphélie la position de mars au moment de l'arrivée. Le demi grand-axe est donc voisin de 1.262 UA, moyenne des demi grands axes de la terre et de mars, et la durée du voyage, découlant de la troisième loi de Kepler, est la moitié de la racine carrée du cube de 1.262 soit 0.7 année ou 260 jours en moyenne.
Mais on ne peut pas partir quand on veut: au départ la terre, plus rapide, doit être derrière mars et devant lui à l'arrivée. Les dates de départ et d'arrivée doivent donc encadrer une opposition.
C'est là que les oppositions prennent toute leur importance: il faut partir environ 100 jours avant l'opposition pour arriver 160 jours après.
C'est ainsi que Curiosity a utilisé l'opposition du 3 mars 2012 en partant le 26 novembre 2011, soit 98 jours avant, et en arrivant le 6 août 2012, soit 156 jours après. Le voyage a duré 254 jours.
L'opposition du 8 avril 2014 avec un départ en novembre 2013 et une arrivée en septembre 2014 a été exploitée par la NASA (mission MAVEN) et par l'ISRO, Indian Space Research Organisations, (mission MOM).
Les deux prochaines oppositions permettront les voyages illustrés ci dessous.

voyage vers mars en 2016

voyage vers mars en 2018/2019

 

déplacements écliptiques des 7 astres mobiles, soleil, lune, planètes

Déroulons l'écliptique, gardons le soleil au centre et, au fil des jours de l'année 2014, marquons les positions de la lune, des dragons (nœuds de l'orbite lunaire) et des planètes. Les planètes ne sont pas exactement sur l'écliptique en raison de leur latitude (sauf quand elles passent aux nœuds de leur orbite). Autour des dragons les zones dangereuses pour le soleil figurent en rouge et ces zones sont reportées sur l'axe vertical décrit par le soleil.
A tout instant seule la moitié de l'écliptique est visible pour l'observateur terrestre: la moitié invisible est caviardée. Vers le milieu de la partie visible et à une distance de ce milieu qui évolue dans la journée (nulle à midi solaire) se trouve le point d'intersection de l'écliptique et du méridien central du lieu d'observation (ici SION en Suisse) ainsi qu'un segment figurant l'amorce de ce méridien et montrant à tout instant l'angle séparant les plans de ces deux cercles.
Des courbes harmonieuses apparaissent, pleines d'enseignement: mercure, toujours proche du soleil, virevolte d'assez près, vénus, étoile du matin presque toute l'année 2014, garde ses distances, les courbes des planètes extérieures sont plus linéaires. La lune suit la courbe pointillée en forme de vague qui décrit tout l'écliptique en un mois lunaire. La forme sinueuse de cette courbe est due à l'importante inclinaison de l'orbite lunaire et elle traverse l'écliptique quand la lune retrouve les dragons qui eux vont en ligne quasiment droite.

On peut voir sur ce tableau les meilleurs dates d'observation pour mercure et vénus: elles correspondent à leur élongation au soleil maximum (pour mercure l'inclinaison de l'orbite et l'angle entre l'écliptique et l’horizon pénalisent les mois de mars et septembre).

On peut apprécier sur les bords du tableau les jours des oppositions des planètes supérieures: 5/01 pour jupiter, 8/04 pour mars, 10/05 pour saturne.

La diagonale tracée du haut à gauche au bas à droite donne la pente d'un astre qui suivrait exactement le soleil. En comparant visuellement cette pente aux courbes des planètes on constate que mars est animé d'un mouvement direct en début d'année (il va plus vite que le soleil) puis qu'il est stationnaire début mars et fin mai, période où il retrouve son mouvement direct. Il en est de même pour saturne, stationnaire début mars et fin juillet. Jupiter commence l'année avec un mouvement rétrograde puis est stationnaire début mars et début décembre où il retrouve son mouvement rétrograde.

A droite du tableau sont reportées les orbites des planètes dans leurs dimensions relatives ainsi que leurs positions. On peut noter les excentricités importantes de mars et surtout de mercure et celles, moyennes, de jupiter et saturne.

18 août 2014  6h jupiter et vénus se lèvent ensemble

Au mois d'août 2014 se produit un resserrement des planètes autour du soleil: vues depuis la terre elles se rassemblent dans un secteur d'environ 100° et il se produit trois conjonctions planétaires en l'espace de moins de 25 jours. Mercure se rapproche à moins de 1° de jupiter le 2/08 puis c'est vénus qui s'en approche à moins de 0.2° le 18/08 et le 27/08 saturne et mars sont à 3.5° l'une de l'autre. Cependant une conjonction n'est observable que si le soleil n'est pas de la partie. Les conjonctions de mercure sont ainsi souvent impossibles à observer à l’œil nu: c'est le cas de celles du 2 août et du 26 novembre.
Avant le 18 août vénus se lève avant jupiter, le 18, les deux planètes se lèvent ensemble à 4h55, heure légale, plus d'une heure et demi avant le soleil. Vénus est bien plus brillante (-3.3) que jupiter (-1.3). Le spectacle, qui mérite le détour, se déroule à l'est à l'azimut -107° et dure une heure avant que le soleil vienne éteindre nos stars. Après le 18, jupiter précède vénus lors du lever.
 

31 août 2014  la lune, saturne et mars passent la journée ensemble

A cette période, le soir, dès 21h, mars et saturne entrent en scène:  elles se couchent vers 23h, deux heures après le soleil, mars d'abord, saturne ensuite. Elles ont la même magnitude 0.8 et brillent au sud-ouest. Le 27, elles sont au plus près l'une de l'autre. La lune se rapproche d'elles jour après jour (la nouvelle lune a eu lieu le 25) et elle les atteint dans la journée du 31 août. Avec une paire de jumelles on peut s'aider de la lune pour repérer les deux planètes en plein jour et les suivre jusqu'à leur coucher. La lune passe plein sud à 17h49, saturne est à la même hauteur, 2.2° vers l'est et mars 4.2° en dessous et 4.3° vers l'est. Mars se couche à 22h42, la lune et saturne, ensemble à 22h54.

Voilà un mois d'août 2014 peu banal. Serait-ce pour commémorer le centenaire du début de la Grande Guerre?

trois conjonctions vénus-jupiter en 2015 avec mars pour la troisième

double et triple conjonctions 25/27 août 2016

la découverte de l'organisation du système solaire: le génie de Kepler

Pour les civilisations très anciennes, les 5 planètes, astres mobiles, sont des divinités qui semblent divaguer à leur guise. Puis les philosophes et savants grecs estiment qu'elles obéissent à des règles suprêmes commandées par les dogmes du cercle parfait et de l'uniformité des mouvements. 
Claude Ptolémée (90-168), faisant la synthèse des conceptions de l'époque, décrit l'organisation du système solaire qui va être en vigueur pendant 15 siècles dans "La Composition Mathématique", ouvrage traduit en arabe sous le nom "la très grande...", c'est à dire "Almageste", puis, après la perte de l'original grec lors des invasions, traduit à nouveau en latin à partir du 13ème siècle. 
La terre immobile est placée au centre de l'univers, le soleil décrit un cercle excentré par rapport à la terre, les planètes décrivent des cercles épicycles centrés eux-mêmes sur des cercles déférents de diamètres variés, convenablement inclinés, dont les centres sont excentrés par rapport à la terre. Un point appelé équant, symétrique de la terre par rapport au centre du déférent, détermine la vitesse angulaire uniforme de la planète. Cette usine à gaz semble indessinable!
Cependant le système de Ptolémée est en conformité avec les observations, au degré de précision près de celles-ci, mais l'absurdité de la non-rotation de la terre sur elle-même est gommée.
L'héliocentrisme n'était imaginé que par quelques minoritaires. Archimède (-287/-212) cite ainsi Aristarque de Samos (-320/ -250).
Après des siècles de silence la science astronomique occidentale se réveille avec le chanoine polonais Nicolas Copernic (1473-1543), aussi médecin et astronome, qui propose, mais sans preuve et sous le manteau, d'améliorer l'explication de Ptolémée en abandonnant le géocentrisme au profit de l'héliocentrisme ce qui permet de supprimer l'artifice des points équants. Il ressuscite ainsi les thèses des minoritaires grecs rentrées en grâce dans les milieux intellectuels de la fin du Moyen Age.
Mais le nombre important des cercles nécessaires pour valider la marche des planètes n'est guère compatible avec la simplification revendiquée.
La bataille, d'ordre philosophique plutôt que scientifique, commence entre les tenants de Ptolémée et ceux de Copernic dont l’œuvre, parue à sa mort, "De Revolutionibus Orbium Coelestium", est condamnée aussitôt par Luther puis en 1616 par le pape. 
Plus de 50 ans après la publication de l’œuvre de Copernic, en 1596, Johannes Kepler (1571-1630), jeune mathématicien allemand partisan de Copernic, fait paraître "Mysterium Cosmographicum", un traité expliquant l'architecture des planètes autour du soleil à partir de spéculations quasi-mystiques sur les polyèdres réguliers...
Tycho Brahé (1546-1601), astronome danois et observateur hors pair fut intéressé par le livre et lorsqu'il doit se réfugier à Prague en 1600, il propose à Kepler, lui-même pourchassé par la persécution religieuse, de l'y rejoindre. Il lui confie alors le problème jugé inextricable de modéliser l'orbite de la planète Mars, à partir de ses très précises observations.
La Science a de la chance car Mars est la planète dont l'excentricité est la plus forte, à l'exception toutefois de Mercure, mais cette planète, toujours peu éloignée du soleil, est difficile à observer surtout dans les frimas danois.
Mars va trahir le vrai secret cosmographique et le génie de Kepler va changer l'Histoire.
Dix années de calculs, de réflexions, d'intuitions seront nécessaires de 1600 à 1609.
Remettant d'abord le soleil vrai et non le soleil moyen de Copernic au centre de l'orbite de Mars il montre la stabilité de l'angle entre les plans des orbites de mars et de la terre (l'existence de cet angle complique grandement les calculs). Cela corrobore son intuition d'un soleil qui ferait se mouvoir les planètes.
C'est donc bien ce soleil vrai qu'il faudra considérer par la suite.
Puis, ayant constaté que plusieurs positions de Mars sont incompatibles avec une orbite centrée sur le soleil, il calcule l'excentricité à lui donner et constate que celle-ci est variable, ce qui est inconcevable! Conclusion: l'orbite n'est pas un cercle.
Devant les complications qui s'annoncent et pour être en terrain sûr, Kepler veut vérifier que les hypothèses faites sur la position de la terre à partir de laquelle sont évidemment faites les mesures des positions de Mars, n'introduit pas un biais par rapport au soleil. Il imagine ainsi de calculer l'orbite de la terre à partir de Mars! C'est possible car tous les 687 jours cette planète revient au même point de l'espace alors que la terre dans le même temps progresse d'un tour et 10/12 de tour. Il constate alors que l'orbite de la terre est une sorte de cercle un peu aplati et légèrement excentré par rapport au soleil. Il constate aussi que la planète va plus vite quand elle est près du soleil et moins vite quand elle en est le plus éloignée. Il pense à une relation inversement proportionnelle entre vitesse et distance.
Ensuite, sans percer le mystère de cette orbite, et reprenant l'hypothèse du cercle excentrique, il a l'intuition d'évaluer, par une sorte de calcul différentiel avant l'heure, la surface balayée par le rayon et découvre ainsi sa deuxième loi (avant la première): cette surface est proportionnelle au temps.
Quelle révélation a du être pour lui cette découverte, et quelle jubilation!
Il est le premier à connaître la vraie loi fondamentale qui organise l'univers!
Mais l'enjeu est l'orbite de Mars, alors il reprend les calculs des positions de Mars sur ces nouvelles bases et constate qu'il faut sans ambiguïté rejeter la solution du cercle: chaque position conduit à un cercle différent...
L'orbite est donc une figure ovale, une sorte d’œuf. Reste à préciser la forme exacte de cet ovoïde!
Kepler s'acharne alors à examiner les résultats que donnent diverses hypothèses faites sur l'excentricité et ne débouche sur rien. Il se résout enfin à tracer point par point l'orbite à partir des positions calculées: l'ellipse lui crève les yeux mais il ne la voit pas!
A l'issue de considérations géométriques plus ou moins absconses sur l'ellipse car il veut théoriser la courbe obtenue, il se rend à l'évidence : l'orbite est une ellipse dont le soleil est un foyer.

Kepler a réussi: Mars est son "très noble prisonnier...acquis...en un combat difficile et laborieux", comme il l'écrit en 1609 dans "Astronomia Nova" qui est un véritable reportage sur cette bataille.

La troisième loi est révélée presque accidentellement en 1619 dans "Harmonices Mundi" qui reprend les considérations quasi-mystiques du premier livre de Kepler.
On peut d'ailleurs s'étonner de ce que cette loi qui établit la proportionnalité entre le cube du rayon moyen de l'orbite et le carré de la durée de la période de révolution n'ait pas été énoncée plus tôt par un astronome gagné à l'héliocentrisme et imaginatif, occidental, arabe ou grec, car elle ne découle pas des deux premières lois et ne nécessite que des calculs simples. Elle aurait été un argument de poids pour l'héliocentrisme!

Bien sûr ces lois ne sont qu'expérimentales, ce que regrette Kepler, mais la science mathématique de l'époque ne permet pas d'aller plus loin et c'est Newton (1643-1727) qui montrera en 1686, 80 ans plus tard, dans "Principia Mathematica" que ces 3 lois sont, ensemble, les conséquences de l'attraction universelle inversement proportionnelle au carré de la distance.

l'orbite de mercure et l'hodographe de son mouvement

 L'excentricité de l'orbite de mercure, 0.2056, est bien plus importante que celle de mars, 0.0934, (celle de la terre vaut 0.01671) et, en proportion, les foyers de l'ellipse de mars sont 2.2 fois plus rapprochés que ceux de mercure et l'épaisseur de la "lunule" entre cercle et ellipse de mars au voisinage du petit axe n'est que 20% de celle de mercure. L’écart entre grand et petit axe n'est que 0.0044!
C'est dire la précision qu'il fallait obtenir dans les observations et les calculs! 

Kepler a cherché à expliciter la position de la planète en fonction du temps, mais ni la géométrie ni la trigonométrie n'étaient alors assez développées. De plus les successeurs de Kepler ont constaté qu'on ne peut relier directement le temps et l'angle de position et qu'il faut passer par une variable intermédiaire. Soit m' le point du cercle principal de l'ellipse qui donne par affinité le point où se trouve mercure, cette variable intermédiaire est l'angle, mesuré depuis le centre du cercle, que fait la direction de ce point m' avec la direction du périhélie. On l'appelle l'anomalie excentrique, notons le "u".
Sur la figure sont marqués en bleu l'angle de position appelé anomalie vraie, notons le "v", en gris l'angle équivalent au temps appelé l'anomalie moyenne, notons le "M" et en rouge l'anomalie excentrique u.
La question est de formuler la loi des aires avec ces variables. Le calcul de la surface balayée depuis le centre par le point m' fait intervenir le sinus de l'angle u et en y retranchant la surface du triangle centre/soleil/m' on obtient la surface balayée depuis le soleil par le point m' en fonction de l'anomalie excentrique. La surface balayée par la planète lui est proportionnelle dans le rapport des axes. Tous calculs faits l'équation de la loi des aires s'écrit: u-sin(u)=M, c'est une équation transcendante soluble par itération ou par emploi de séries. Il reste à relier v et u, cela se fait en calculant d'abord la longueur du rayon vecteur en fonction de u et de v, puis en torturant les égalités obtenues au moyen des formules de trigonométrie, un peu comme fait celui qui invente des "colles de trigo" à poser à ses élèves. On trouve, entre autres, que les tangentes des demi anomalies, vraie et excentrique, sont liées par un coefficient de proportionnalité, simple fonction de l'excentricité.
Ainsi, pour un instant M, on résout d'abord l'équation de Kepler puis on calcule l'angle de position et, en prime, le rayon vecteur.
C'est si simple que Kepler pourrait se retourner de joie dans sa tombe, mais il n'y a pas de tombe de Kepler, seulement un monument à Ratisbonne où est gravée l'épitaphe qu'il avait composée lui-même (en latin): 

Moi qui ai mesuré les cieux, je mesure maintenant les ombres de la terre

L'esprit était céleste, ici gît l'ombre du corps

Comparons la marche de mercure sur son orbite à partir du périhélie à celle d'un mobile à rotation uniforme qui se retrouverait au bout d'une révolution de mercure au périhélie en même temps que la planète. Au départ la vitesse de mercure dépasse sensiblement celle du mobile et la planète prend de l'avance. L'écart entre les deux (anomalie moyenne du mobile et anomalie vraie de mercure) s'appelle l'équation du centre. Quand mercure a fait un quart de tour, son concurrent n'en est qu'à un sixième et l'écart s'accroît jusqu'au point m1 où il est maximum et vaut 24°. Ce point précède le moment où mercure passe au sommet du petit axe. L'écart diminue alors à partir du point m1 et au point m3 mercure se trouve à mi-chemin de l'aphélie en terme de temps. Le mobile rattrape mercure à l'aphélie et lui passe devant: il va faire la course en tête jusqu'au périhélie, de façon symétrique.
Les parties hachurées représentent l'une la surface balayée en 1 jour quand la planète est proche du périhélie, l'autre quand elle l' est de l'aphélie: ces surfaces sont égales.
Marquons F le deuxième foyer de l'ellipse: ce point n'est rien d'autre que le point équant de Ptolémée!
La vitesse linéaire de la planète, si chère à Kepler, s'exprime très simplement en fonction des rayons vecteurs de la planète depuis le soleil et depuis le point équant: elle est proportionnelle à la racine carrée de leur rapport. Cela signifie, entre autres, qu'en 2 points de l'orbite symétriques par rapport au petit axe, le produit des vitesses est une constante.
Une autre caractéristique est que cette vitesse de la planète est inversement proportionnelle à la distance du soleil à sa projection sur la tangente à l'orbite. Cette distance n'est jamais très différente du rayon vecteur, ce qui explique l'idée de Kepler d'une proportion inverse à ce dernier. La valeur du produit de la vitesse par cette distance est égale au double de la surface de l'orbite divisée par la période.
 Au périhélie la vitesse de mercure est de 58.98 km/s et à l'aphélie 38.86 km/s, la moyenne géométrique de ces deux valeurs est 47.87 km/s: c'est la vitesse de mercure quand elle est au sommet du petit axe. C'est aussi la vitesse d'un mobile régulier qui décrirait le cercle principal de l'ellipse avec la période de mercure. En effet 47.87 km/s équivaut à 0.02765 UA par jour (UA=unité astronomique=149.598.000 km). En divisant le périmètre du cercle principal de l'ellipse dont le rayon est pour mercure 0.3871 UA, par cette vitesse, on trouve 87.97 jours qui est la période de révolution de mercure! Magie de Kepler?
L'hodographe du mouvement képlerien, c'est à dire le lieu de l'extrémité d'un vecteur égal au vecteur vitesse, dont l'origine serait fixe, est très particulier: c'est un cercle ici dessiné en vert. Ainsi ce n'est pas le mouvement qui est circulaire mais la dérivée de celui-ci. Belle revanche pour Aristote!
La vitesse moyenne de la planète ne se livre pas facilement car si on connait cette vitesse à tout instant, par contre le périmètre de l'ellipse ne peut être calculé sans avoir recours à l'intégrale elliptique de deuxième espèce...La valeur approchée est 47.35 km/s (pour la terre: 29.78 km/s et pour mars 24.08 km/s). Mercure est alors au point m2.
L’observation attentive de la figure montre que le rayon vecteur issu du point équant, mieux appelé point d'égalité, reste pratiquement parallèle au rayon vecteur du mobile à rotation uniforme. Ce n'est pas une illusion: le calcul montre que l'écart est du deuxième ordre en fonction de l'excentricité. Pour mercure il ne dépasse pas 0.74°.
C'est ainsi qu'en première (et bonne) approximation certains astronomes du XVII ème siècle purent s'affranchir de la terrible équation de Kepler en calculant l'anomalie vraie directement à partir de l'anomalie moyenne sans passer par l'anomalie excentrique. L'erreur ainsi induite sur l'anomalie vraie varie de -35.3' à +40.5' pour mercure et de -7.3' à +7.9' pour mars, ce qui dépasse la précision des observations de Tycho Brahé.
Cette façon de faire valide en quelque sorte le principe de l'équant et constitue un hommage à Ptolémée!

Mercure, le tour du soleil en 88 jours