Modèlisation des marées océaniques

le Couesnon en sa folie a mis le Mont en Normandie (Chateaubriand)

 La marée, ou plutôt le marnage, peut atteindre, en certains points des côtes, des valeurs impressionnantes: 13 m en Europe dans la baie du Mont Saint Michel et 16 m dans la baie de Fundy en Nouvelle Écosse aux confins du Canada, des États-Unis et de Saint Pierre et Miquelon. Ces records sont dus à des particularités de la côte: en océan ouvert le marnage n'atteint pas un mètre.

Le phénomène induit sur la Terre par la Lune et le Soleil résulte de la loi de la gravitation universelle, établie par Isaac Newton (1703/1727) sur la base des trois lois de Johannes Kepler (1571/1630): deux corps s'attirent entre eux en fonction du produit de leurs masses et de l'inverse du carré de leur distance. Des forces considérables sont ainsi à l’œuvre à la surface de la Terre et l'énergie dépensée est empruntée à la rotation terrestre qui ralentit en conséquence d'environ 2 millisecondes par siècle. L'effet corrélatif sur la Lune correspond à un éloignement d'environ 3,8 cm par année.

Le moulin du Birlot à l'île de Bréhat en Bretagne

Les moulins à marée et les usines marémotrices mettent à profit l'énergie des marées

l'usine marémotrice de la Rance en Bretagne

La Terre subit à la fois l'attraction de la Lune et celle du Soleil. C'est la combinaison des deux qui détermine la marée.

L'écart de distance de l'astre attracteur avec le centre de la Terre d'une part, et avec un point de sa surface d'autre part, caractérise la force de marée en ce point. En désignant par D la distance de l'astre à l'axe de la Terre et par d la distance du point choisi à cet axe on peut calculer la différence d’attraction à partir de la loi de Newton. Au point choisi l'attraction sera K*T*A / (D - d)^2 et au centre de la Terre K*T*A / D^2, A désignant la masse de l'astre, T celle de la Terre, le coefficient K dépendant des unités choisies.

L'écart d'attraction est donc K*T*A (1 / (D - d)^2 - 1 / D^2), soit K*T*A (2d * D - d^2) / (D^2 * (D - d)^2).

Mais la distance d (6378 km au plus) étant très faible relativement à la distance D (356.500 km au moins pour la Lune, 147.100.000  km au moins pour le Soleil), on peut négliger le terme en d^2, assimiler D - d à D et donc écrire que l'écart d'attraction est proportionnel à K*T*A (2d*D / D^4) soit K*T*A (2d / D^3).

La force de marée en un point de la surface de la Terre est donc proportionnelle à la distance de ce point à l'axe terrestre et à la masse de l'astre attracteur et inversement proportionnelle au cube de la distance de cet astre.

Deux corps célestes bien inégaux sont à la manœuvre pour la Terre (l'influence de la planète qui s'approche le plus, Vénus, ne représente que la dix millième partie de celle du Soleil). Le rapport entre les masses du Soleil et de la Lune est de 27.000.000 et celui entre leurs distances de 400. On obtient alors comme écart entre l'attraction induite par la Lune et celle induite par le Soleil en un point quelconque de la Terre: 400^3 / 27.000.000 soit 64.000.000 / 27.000.000 soit 2,4.

Newton, avec les connaissances de l'époque, avait chiffré la marée lunaire à 2,2 fois la marée solaire.

De toute façon, la distance Terre / Lune variant entre 356.500 km et 406.700 km et la distance Terre / Soleil entre 147.100.000 km et 152.100.000 km, le rapport des distances varie entre 326 et 427, ce qui conduit à des valeurs extrêmes du rapport marée lunaire / marée solaire de 1,8 et 2,9.

Au périgée minimum la force de la marée lunaire dépasse de 48% celle à l'apogée maximum. Pour la marée solaire l'écart entre périhélie et aphélie est 10,5%.

 Le critère déterminant de l'importance de la marée lunaire, et donc de la marée totale, est la distance Terre Lune.

 

Dans la suite on s'intéresse à une Terre fictive, sphérique, sans rotation sur elle-même et qui serait entièrement recouverte d'un matériau homogène de très faible viscosité, l'orbite de la Lune se situant dans le plan de l'écliptique. Ces hypothèses permettent d'établir un modèle géométrique utile à la compréhension du phénomène de la marée.

La déformation due à une force de marée donne à la surface de la Terre l'aspect d'un ellipsoïde.

l'ellipsoïde de marée

Soit un point P d'un méridien terrestre repéré par sa latitude notée lat (angle en gris). On a vu plus haut que la force attractive représentée par le segment PE est proportionnelle au segment PA. Or on a là une propriété de l'ellipse d'axes a et b: AP = bcos(lat), AE = acos(lat). D'où PE = (a - b)cos(lat). L'attraction exercée par l'astre attracteur ne dépend que de la latitude et donne ainsi à la surface terrestre la forme d'un ellipsoïde. Dans le référentiel centré au point P, reporté en O, et dont les axes sont l'horizon et la verticale, l'attraction est représentée par le segment OF. En faisant varier la latitude de -pi/2 à +pi/2 le point F décrit un cercle tangent en O à la direction de l'astre.

La force de marée a donc une composante verticale et une composante horizontale valant celle verticale multipliée par la tangente de la latitude.

Toutes ces considérations s'étendent à un espace en trois dimensions. Elles s'appliquent à la Lune attirée par la Terre et qui présente une forme oblongue dans la direction Terre / Lune. La masse de la Lune n'est que 1/81 de celle de la Terre, soit 0.01234567 (!) et l'effet des forces considérables de la marée terrestre sur la Lune a rapidement abouti au blocage de sa rotation sur la valeur de sa révolution orbitale.

 

Plaçons nous au pôle de l'écliptique, notons v l'écart de longitude entre le Soleil et la Lune (ici 66°). Soit un point P de l'équateur déterminé par son angle horaire h mesuré à partir du Soleil, ici 2h20, soit 35°. Il est alors 14h20 en P.

la Terre vue du pôle de l'écliptique

En rouge, la marée lunaire qui varie de 0 à 83, et en bleu la marée solaire qui varie de 0 à 38.

Quand un astre passe au méridien d'un lieu il exerce une attraction maximale alors qu'à son lever ou à son coucher celle-ci s'annule: l'importance de la marée est une notion locale et instantanée qui dépend d'abord de la hauteur de la Lune dans le ciel et, dans une moindre mesure, de celle du Soleil.

Les deux attractions lunaire et solaire s'additionnent en se composant pour donner une résultante et, en 24h, un lieu donné connait une évolution complète.

Si on note aL le grand axe de l'ellipse lunaire, aS le grand axe de l'ellipse solaire et b leur petit axe commun, l'attraction solaire vaut PS = (aS - b)cos(h) et l'attraction lunaire PL = (aL - b)cos(v - h).

Avec nos hypothèses et à l'échelle de la figure, PS vaut 31 et PL 71.

 L'attraction résultante vaut rac(PS^2 +  PL^2 + 2PS*PLcos(v)).

L'angle w que fait le vecteur représentatif de l'attraction résultante avec l'axe solaire est donné par tan(w) = PLsin(v) / (PS + PLcos(v)).

En désignant par k = (aL-b) / (aS-b) le rapport marée lunaire / marée solaire, l'angle horaire pour lequel la direction du vecteur résultant passe par le centre des ellipses est alors donné par l'équation: 

tan(h) = kcos(v - h)sin(v) / (cos(h) + kcos(v - h)cos(v))

Cette équation se simplifie en la relation:

 tan(2h) = ksin(2v)/(1+kcos(2v))

qui donne deux solutions H et H + pi/2, avec les hypothèses faites: 53° et 143°, soit 15h32 et 21h32.

Pour les lieux correspondants à ces valeurs de l'angle horaire, par hypothèse, l'attraction résultante est verticale et l'attraction horizontale nulle: à l'angle horaire 53° correspond la valeur 92 notée A1 et à 143°, la valeur 28 notée A2. Il en est de même pour leurs valeurs symétriques 233° (3h32) et 323° (9h32).

Plaçons nous alors dans le référentiel local:

référentiel local

 

L'attraction solaire est représentée par le vecteur bleu qui fait un angle, en bleu, égal à l'angle horaire h avec la verticale. Le lieu géométrique de l'extrémité de ce vecteur est le cercle en bleu de diamètre "P/38". Le segment "31/88" fait un angle constant égal à v avec ce vecteur, il passe donc par le point fixe K du cercle tel que l'angle avec l'horizontale soit égal à v.

Le même raisonnement s'applique au vecteur en rouge représentant l'attraction lunaire qui passe donc par le point fixe K' . L'extrémité 88 du vecteur représentant l'attraction résultante décrit donc le cercle en noir passant par les points K, 92, K' et 28 avec les coordonnées:

abscisse : (aS - b)cos(h)sin(h) - (aL - b)cos(v - h)sin(v - h) ordonnée : (aS - b)cos(h)^2 + (aL - b)cos(v - h)^2

Le centre C du cercle a pour ordonnée ((aS + aL) / 2) - b et le rayon est égal à (A1 + A2) / 2.

Soit P' le point d'ordonnée A2. Pour la valeur H de l'angle horaire h, l'extrémité du vecteur de l'attraction résultante, verticale, est au point 92. Il en résulte que l'angle en gris clair P'92K' est égal à H et que l'angle P'88K' qui intercepte le même arc sur le cercle noir garde la valeur fixe H. Cet angle P'88K' est composé de l'angle horaire h en bleu et d'un autre angle en gris foncé égal, car alterne/interne, à l'angle 92P'88.

Il en découle que le segment P'88 fait avec l'axe solaire un angle constant égal à H quand l'angle horaire varie. 

Par ailleurs, le segment P'88 de la figure vaut (A1 - A2)cos(H - h).

Ces deux propriétés démontrent que l'extrémité du vecteur de l'attraction résultante décrit une ellipse dont le grand axe vaut b + A1 et le petit b + A2 et dont le grand axe fait avec l'axe solaire l'angle H qui ne dépend que de l'écart de longitude entre la Lune et le Soleil.

Pour la valeur H de l'heure, les forces de marée verticale et résultante sont égales et maximales, pour H + pi/2 elles sont égales et minimales.

le diagramme de la force de marée

En rouge la force de marée lunaire, en bleu celle du Soleil et en noir la force de marée résultante.

Aux lieux du lever et du coucher de la Lune, l'ellipse résultante est tangente à celle du Soleil car l'attraction lunaire s’annule. De la même façon elle est tangente à l'ellipse de la Lune au moment du lever et du coucher du Soleil.

instant de l'attraction horizontale maximale

Pour certaines heures l'extrémité du vecteur de l'attraction résultante se trouve à une extrémité du diamètre horizontal du cercle décrit. L'attraction horizontale atteint alors son maximum 32, la verticale valant 60. Lors des heures où cela se produit, l'angle CP'68 vaut 45° ce qui signifie qu'il y a un écart de 3 heures avec les passages aux sommets de l'ellipse résultante où cette attraction est soit maximale, soit minimale.

attractions verticale, horizontale et globale sur une moitié du globe

forces de marée verticale et horizontale à un instant donné

au premier et au dernier quartier

à la pleine lune et à la nouvelle lune

 

Les Anciens ont forgé le terme syzygie qui signifie "sous le même joug" pour la configuration où Lune et Soleil sont, vis à vis de la Terre, attelés à la même tâche, c'est à dire soit en conjonction soit en opposition.
 

En première approximation on peut représenter l'intensité globale des forces subies par la couche superficielle de la Terre par la différence de volume entre l'ellipsoïde résultant, en noir, et le volume terrestre, en bleu clair.

Si on se limite à ce qui se passe dans le plan perpendiculaire à l'écliptique, l'énergie globale vaut pi((b + A1)(b + A2) - b^2) et le minimum est atteint lors des pleines ou nouvelles lunes. A ces seuls instants il existe des points au repos sur la Terre: ceux situés sur le méridien terminateur: ils voient en toute sérénité le Soleil et la Lune se lever ou se coucher ensemble ou à l'opposé.

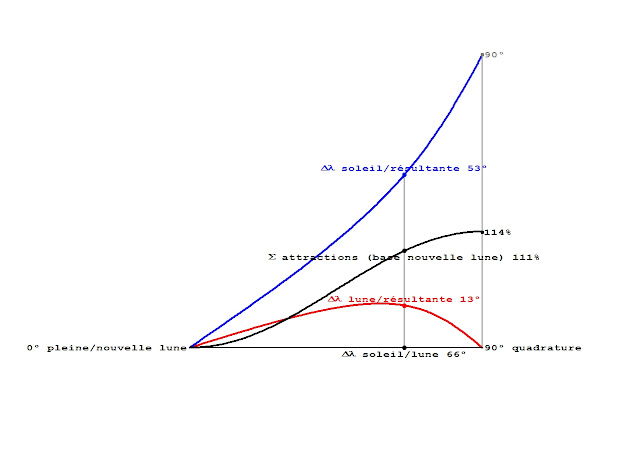à la quadrature la force de marée globale subie par toute la Terre vaut 114% de celle à la nouvelle (ou pleine) lune

 

De la nouvelle (ou pleine) lune à la quadrature l'écart de longitude entre la Lune et le grand axe de l'ellipse résultante passe par un maximum. Celui-ci est atteint pour la valeur notée V qui annule le dénominateur de la formule donnant H, soit cos(2V) = -1 / k et donne ainsi au paramètre H la valeur 45°. Pour cette valeur V, les composantes horizontales des attractions des deux astres sont maximales (et opposées). Au lieu de la Terre où l'angle horaire du Soleil est 45°, soit 3 heures, l'écart angulaire entre Lune et marée résultante atteint son maximum de V - 45°.

pour l'angle horaire 45°, en bleu, les composantes horizontales sont maximales et l'écart angulaire entre Lune et marée résultante est maximal

 

en gris la dérivée, par point, de l'écart angulaire entre Lune et marée résultante

La valeur critique V de l'écart de longitude dépend des hypothèse faites sur l'importance relative des attractions lunaire et solaire, celles-ci donnent ici 58.5°, d'où pour la Lune un angle horaire maximum de -13.5°, soit -54m.

à 15 heures l'écart entre Lune et grand axe commence à diminuer

 

 Les phases de la Lune se succèdent au rythme assez régulier de 29.53 jours. Ainsi, à partir d'une nouvelle lune chaque jour la Lune "remonte " le ciel, en avant du Soleil, de la valeur de 12.2°, ce qui correspond à 49 minutes. A partir de la pleine lune elle rattrape le Soleil au même rythme. Entre deux passages consécutifs au méridien d'un lieu donné il s'écoule donc en moyenne 24heures et 49 minutes.

La figure ci-dessous illustre ce qui se passe pendant cette durée en un lieu où la nouvelle lune se produit à 12h.

Durant 6 heures et 8 minutes la force de marée décroît depuis la valeur maximum de 120 pour atteindre, 8 minutes après le coucher du Soleil, un minimum proche de zéro: 0.1.

La croissance reprend; la Lune se couche à 18h12 et un maximum un peu inférieur à celui du départ, 119.7, est atteint à 0h16, 6 heures et 8 minutes après le minimum.

La diminution reprend (la Lune se trouve à l'opposition à 0h24) et se poursuit jusqu'à 6h24, soit 6 heures et 8 minutes après le maximum, 25 minutes après le coucher du Soleil, jusqu'à un minimum un peu plus élevé que le précédent de 0.7.

L'augmentation reprend alors, la Lune se lève à 6h37, le Soleil passe plein sud à 12h, un maximum un peu inférieur au précédent, 118.8, est atteint à 12h33, six heures et 9 minutes après le minimum.

Entre minima et maxima il s'écoule 6 heures et 8 minutes ce qui conduit à 24 heures et 33 minutes au total.

Après les deux marées hautes et basses, la Lune passe plein sud à 12h49, 16 minutes après la fin du cycle.

La Lune accuse donc bien le retard prévu de 49 minutes, mais pas la marée!

En effet c'est un lieu commun très répandu que d'affirmer que la marée se reproduit avec un retard égal à celui de la Lune! Cela revient à négliger la marée solaire qui intervient pour environ un tiers (entre 25% et 35%) dans le phénomène!

Aux environs de la pleine ou nouvelle lune, le retard de la marée n'est que de 33 minutes car à ce moment, comme le montre la figure précédente, la valeur du paramètre H notée en bleu "soleil / résultante" n'augmente que lentement, en raison de la valeur élevée de la marée solaire, maximum à ces moments.

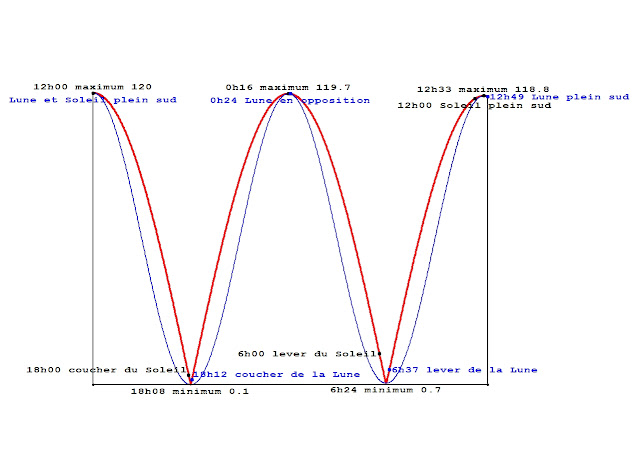lors de la pleine (ou nouvelle) lune le retard de la marée n'est que de 33 minutes

En rouge la force résultante, en bleu la seule force verticale. Vue de la Terre, la Lune prend du retard sur le Soleil: elle se couche et se lève plus tard que lui. Les maxima de la force de marée diminuent alors que les minima augmentent. Cela se poursuivra jusqu'au premier quartier pour s'inverser ensuite jusqu'à la pleine lune.

à la quadrature le retard de la marée atteint 94 minutes

A la quadrature la marée solaire s'annule et change de sens, le paramètre H est égal à 90° et le retard de la marée atteint alors 94 minutes. 

Entre minima et maxima il s'écoule 6 heures et 24 minutes, ce qui conduit à 24 heures et 94 minutes au total.

A partir du premier quartier et jusqu'à la pleine lune les maxima vont augmenter et les minima diminuer.

La figure ci-dessous met en évidence l'évolution des composantes de la force de marée, d'une nouvelle lune à la suivante en un point donné.

 

la force de marée pendant une lunaison de 29.5 jours

 

En haut, en bleu, la composante verticale de l'attraction de la Lune et du Soleil. En dessous, en gris, la composante horizontale.

En bas, en rouge, l'intensité de l'attraction résultante (et non pas sa direction). On constate qu'au voisinage de la nouvelle ou de la pleine lune surtout, la composante horizontale a pour effet de rompre la symétrie de cette attraction en accélérant la variation de l'intensité quand elle est faible ou presque nulle et en la ralentissant quand elle est forte ou maximale.

Pour résumer, la marée théorique fictive la plus considérable doit réunir les paramètres suivants: une nouvelle (ou pleine) lune se produisant avec une Lune au périgée extrême de 356.500 km, un jour proche du périhélie (5 janvier), un lieu où il sera midi solaire (ou minuit) à cet instant avec le Soleil (ou la Lune) au zénith.

Le 14 novembre 2020 à 12h la Lune passe à son périgée à 357.837 km seulement de la Terre et 17h plus tard, le lendemain 15 novembre, c'est la nouvelle lune. Les 15 et 16 novembre 2020 il y a donc de grandes marées (coefficient 109 d'après le SHOM). Il faut attendre les pleines lunes des 28 mars, 27 avril et 26 mai et la nouvelle lune du 6 octobre qui se produisent près du périgée pour connaître des coefficients comparables.

En 2020 et 2021 le périgée se rapproche du périhélie et en 2022 il en restera très proche. Il n'en redeviendra très proche que neuf années plus tard, en 2031. Une nouvelle lune se produit le 2 janvier 2022 à 18h35 TU, 24 heures seulement après son passage au périgée, à 359.000 km. Au point du globe terrestre de longitude ouest 97.7° et de latitude sud 23.4° , à cet instant il est midi solaire et Soleil et Lune (celle-ci invisible) se trouvent au zénith.

Les terres émergées les plus proches semblent être l’île de Pâques de longitude ouest 109.4° et de latitude sud 27.1°et les îles Galápagos de longitude ouest 90.6° et de latitude sud 0.7°. Les côtes les plus proches sont péruviennes et chiliennes.

Circonstances exceptionnelles pour un voyage, mais sans garantie...car il n'y a pas qu'au Plat Pays flamand, que certains "rochers ont à jamais le cœur à marée basse"...

 

Les figures qui suivent présentent les positions les plus intéressantes, avec le dessin des marées, de la Terre, de la Lune et du Soleil pour 

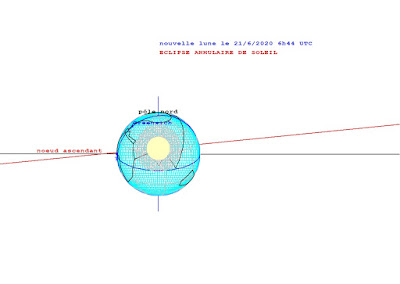
la période s'écoulant de la nouvelle lune du 21 juin 2020 (éclipse annulaire de Soleil) à la pleine lune du 5 juillet 2020 (éclipse de Lune par la pénombre).

 

21 juin 2020 6h40 TU, nouvelle lune et éclipse de Soleil

La Lune est passée au nœud ascendant de son orbite seulement 3 heures avant l'alignement Soleil/Lune/Terre, sa latitude est donc faiblement positive et l'éclipse peut être observée dans l'hémisphère nord aux latitudes peu élevées.

L'éclipse est annulaire car, à la fois, la Lune entre apogée et périgée se tient à une distance moyenne de 387.900 km et la Terre, proche de son aphélie du 4 juillet, donc plutôt loin du Soleil se trouve à 152.031.400 km de lui. Le diamètre apparent du Soleil, 31.5', dépasse de 2% celui de la Lune, 30.8'.

La marée est moyenne/supérieure.

Au moment des éclipses les marées atteignent de grands coefficients puisque les deux phénomènes ont un opérateur commun: la Lune.

 

24 juin 2020 14h45 TU, la Lune passe au méridien de Greenwich

 

25 juin 2020 15h38 TU, la Lune passe au méridien de Greenwich

Entre les deux passages consécutifs de la Lune au méridien de Greenwich, il s'est écoulé 24 heures et 53 minutes.

Cet écart de 53 minutes correspond au déplacement de la Lune sur son orbite entre deux passages au méridien, écart plus ou moins important selon qu'elle se trouve loin ou près de son périgée.

28 juin 2020 8h TU, premier quartier

5 juillet 2020 4h58 TU, pleine lune et éclipse par la pénombre

La Lune est passé la veille, 4 juillet à 3h TU, au nœud descendant de son orbite et sa latitude négative vaut -1.3° ce qui la fait échapper à l'ombre elle-même de la Terre.

La demi lunaison du 21 juin au 5 juillet a duré 13 jours et 22 heures ce qui est bien moindre que la moyenne de 14 jours et 18 heures (29.53 / 2), ceci parce que la Lune a traversé le périgée le 30 juin ce qui lui confère un déplacement rapide. Pendant ce délai la longitude du Soleil a progressé de 13.3 degrés ce qui est moindre que la moyenne de 13.7 degrés, ceci parce que la Terre a traversé l'aphélie le 4 juillet là où son déplacement est moins rapide.

La marée est moyenne/supérieure comme lors de la nouvelle lune.

 

 

les marées dans la réalité vue par les satellites

 

Le modèle des marées développé plus haut doit évidemment être sensiblement affiné parce que l'orbite de la Lune est incliné sur l'écliptique et pour tenir compte de la rotation de la Terre, de l'inclinaison de son axe de rotation, de la latitude du lieu, de la disposition, de l’épaisseur et de la viscosité différentielles des matériaux composant la couche superficielle.

On peut cependant considérer que l'inclinaison de l'orbite lunaire ne remet pas fondamentalement en cause les résultats obtenus.

La rotation de la Terre autour d'un axe incliné semble être la cause d'un accroissement de la marée en période d'équinoxe parce qu'alors la force centrifuge terrestre est le plus colinéaire avec les forces de marée ce qui les renforce.

La viscosité des eaux, surtout si elles sont peu profondes, entraîne un retard du "bourrelet" de marée par rapport à la direction de la Lune et un décalage de l'heure de la marée par rapport à l'angle horaire de la Lune.

Quant au découpage des côtes qui génère des phénomènes ondulatoires, à lui seul, il interdit toute théorie d'ensemble précise.

 

la Terre dans le viseur de la Lune, NASA mission Apollo

Mars: ça repart...

un être animé sur Mars?

Le 14 décembre 1962, pour la première fois, une planète du système solaire était survolée par une sonde: c'était Vénus et Mariner II (voir à ce sujet l'article du présent blog en date du 20/11/2018 intitulé "L'époque héroïque de l'exploration du Système Solaire").

Deux ans plus tard, l'exploration de la planète Mars commençait avec le lancement le 28 novembre 1964 de la sonde Mariner IV qui l'a survolée le 14 juillet 1965 et qui est devenue une micro-planète du système solaire. La NASA a ainsi profité de la fenêtre ouverte par l'opposition du 9 mars 1965.

L'architecte allemand Walter Hohman (1880/1945) a identifié le premier, en 1925, la trajectoire optimale d'un voyage dans l'espace. Pour un voyage interplanétaire depuis la Terre, il faut décrire la demi ellipse qui a pour foyer le Soleil, pour distance périhélique (aphélique) le rayon vecteur de la Terre et pour distance aphélique (périhélique) celui de la planète. Il faut partir avant une opposition pour arriver après celle-ci.

Mars tourne sur elle-même en  24h39.38m, elle décrit son orbite en 668.6 sols martiens ce qui correspond à 686.98 jours terrestres. Sa révolution synodique moyenne qui ramène les deux planètes dans la même configuration solaire compte 780 jours mais elle varie fortement entre 764 jours et 811.
En effet l'ellipse décrite par Mars présente une assez forte excentricité, 0.0933, soit 5.6 fois celle de la Terre, 0.0167. Il en résulte un aphélie à 1.666 UA du Soleil, soit une opposition aphélique à 0.67 UA de la Terre et un périhélie à 1.381 UA du Soleil, soit une opposition périhélique à 0.38 UA de la Terre.

Selon la loi de la gravitation universelle, dans le système solaire, la vitesse V et la distance r d'une planète sont liées  par la relation:

V = 29.785 * rac ( 2 / r - 1 / a ) km/s où a est le demi grand axe de l'orbite en UA.

Pour Mars la vitesse au périhélie atteint 26.5 km/s, pour 22 km/s à l'aphélie. En conséquence la durée d'une révolution synodique varie en fonction des positions successives de Mars sur son orbite au moment des oppositions.

La longitude du second foyer, le premier étant le Soleil, est de 334°. Une opposition à l'aphélie se produit donc vers le 22 février et une opposition au périhélie vers le 27 août.

 Quinze ans comptent 5479 jours alors qu'il faut à Mars 5496 jours, soit 17 jours de plus, pour décrire huit fois son orbite. Il en découle un rythme imparfait de 15 ans pour la survenance des oppositions.

trajectoire de Mars et oppositions dans un repère terrestre, de mars 2012 à février 2027

Pour survoler la planète il est intéressant de choisir une opposition lors de laquelle Mars est proche de la Terre, opposition périhélique, car alors la vitesse d'injection à communiquer au départ sera moindre.
Mais, si on veut, non plus seulement survoler la planète mais s'y poser en douceur, il faudra, à l'arrivée, imprimer au vaisseau une décélération, d'autant plus élevée et coûteuse en énergie embarquée que Mars sera moins rapide et donc plus éloignée du périhélie.

Au fur et à mesure que la puissance des lanceurs progresse ces considérations perdent de leur pertinence mais les oppositions les plus favorables restent celles qui se produisent entre juin et novembre.
L'opposition du 15 décembre 1975 a permis à la NASA de poser sur Mars pour la première fois en juin et août 1976 deux atterrisseurs Viking après un long voyage de 10 et 11 mois.
Celle du 17 mars 1997 a vu la dépose du premier rover Sojourner après un voyage de 240 jours.

L'opposition exceptionnelle du 28 août 2003 qui a mis Mars à 0.38 UA seulement de la Terre a permis à la NASA d'envoyer avec succès deux rovers sur Mars à 27 jours d'intervalle les 10 juin et 7 juillet 2003. Spirit et Oppotunity sont arrivés à destination en janvier 2004 après 200 jours de voyage.

Huit années et demi plus tard, après un report du lancement de 2009 à 2011, c'est en utilisant l'opposition défavorable du 3 mars 2012 (Mars à 0.67 UA de la Terre) que la NASA dépose sur Mars le rover Curiosity, preuve des progrès intervenus dans les capacités des lanceurs. Le lancement a eu lieu le 26 novembre 2011 et l'arrivée le 6 août 2012 après un voyage de 254 jours.
L'atterrissage sur Mars est rendu compliqué par une gravité assez forte de 3.71 m/s^2 et une atmosphère de faible densité au niveau du sol, 6 millibars. La Lune, sans atmosphère, présente une gravité de 1.62 m/s^2 seulement. Pour la Terre, la gravité est forte, 9.81 m/s^2, mais la densité de l'atmosphère atteint 1015 millibars au niveau de la mer.
L'étude du projet avait commencé dès 2003 et a mis en œuvre des techniques d’atterrissage combinées avec parachute, rétro-fusées et grutage final en douceur sur le sol martien.
Le rover Curiosity est un véritable laboratoire mobile (MSL) commandé en direct et en aveugle par des équipes qui sont éloignées, au mieux, de 57 millions de kilomètres et, au pire, de 400 millions.

Aujourd'hui il continue à fonctionner et provoque, à coup sûr, la perplexité des martiens qui le voient évoluer...

1997: Sojourner 11 kg, 2004: Oppotunity et Spirit 174 kg, 2012: Curiosity 900kg (2021: XXX 1050 kg?)

A l'assaut du mont Sharp 5.500 m.

 

L'opposition favorable du 13 octobre 2020 va être utilisée au cours de l'été pour plusieurs missions.

Avec Mars 2020, les États-Unis reconfigurent le laboratoire MSL de 2011 en le fiabilisant et en l'améliorant pour lui permettre de stocker des échantillons du sol martien en vue de leur retour sur Terre à l'horizon 2026! Le lancement aura lieu le 17 juillet 2020 pour une arrivée le 18 février 2021 (216 jours).

L'ESA, alliée à la Russie, après la première phase de la mission ExoMars lancée le 14 mars 2016 qui a connu la réussite de l'orbiteur TGO mais aussi l'échec de l'atterrisseur Schiaparelli qui s'est écrasé sur Mars le 19 octobre 2016, prévoit un lancement fin juillet / début août 2020 pour une arrivée en mars 2021. Le lanceur et l'atterrisseur seront russes et le rover européen.

La Chine pour sa mission HX-1 utilisera son lanceur Longue Marche 5 pour amener sur Mars un orbiteur, un atterrisseur et un rover.

Un lanceur japonais mettra sur orbite un engin étudié par les Émirats arabes unis en collaboration avec deux universités américaines.

Toute cette effervescence autour de la planète rouge relance l'idée d'un séjour humain et même d'une "colonisation".

Mais si le principe de l'opposition Terre-Mars commande les dates du voyage aller, il en est de même pour le voyage retour.

voyage aller de la mission américaine Mars 2020

L'arrivée sur Mars intervient le 18 février 2021 et pour revenir sur Terre il faut attendre la prochaine opposition qui a lieu le 8 décembre 2022, 786 jours après l'opposition du 13 octobre 2020.

Ce qui fait prévoir de quitter Mars au début du mois d'août 2022 pour une arrivée sur Terre vers le milieu du mois de mars 2023.

voyage retour le plus proche possible

Parti le 17 juillet 2020 de la Terre, l'astronaute y revient quelques 1.000 jours après, en mars 2023!

Près de 1.000 jours de voyage, dont 500 environ passés sur Mars et presque autant dans un vaisseau spatial.

"L'écologie décoloniale établit des horizons non extractivistes: c'est une écologie du renoncement. Dans les cosmologies occidentales, ne serait-ce que par la pensée, on peut tout faire. Or je crois qu'on ne peut pas coloniser la Lune, le ciel, Mars, juste parce-qu’ils sont vides."

Diego Landivar directeur de "Origens Media Lab" à Clermont-Ferrand,
cité par "Le Monde" daté 25 janvier 2020.

Année 2020, la planète Mars comme objectif

2020, une bonne année pour Mars.

Les missions vers Mars devront partir au mois de juillet pour profiter de la meilleure proximité de la planète qui a lieu le 6 octobre, l'opposition se produisant le 13. Ce décalage est du à la latitude géocentrique négative de Mars à cette période: -3.3°. La planète passera à son nœud ascendant début décembre.

Les PLANÈTES en 2020

Mercure fait ses quatre apparitions annuelles et rencontre Vénus fin mai.
Vénus est une très belle étoile du berger le soir jusqu'en juin puis le matin après l'opposition du 3 juin.
Tout au long de l'année Jupiter et Saturne restent voisines, le matin de mars à juillet, puis le soir d'août à novembre. Mars leur rend visite le matin vers la fin du mois de mars.

la trace de la Lune a été fortement exagérée, en réalité sa concavité est toujours tournée vers le soleil

La figure ci-dessus présente la course, au cours de l'année 2020, des planètes, de la Lune et des nœuds de l'orbite lunaire.
La distance de la Lune à la Terre a été amplifiée pour mettre en évidence les moments des pleines lunes et des nouvelles lunes et pour rendre compte de la variation, entre pleine et nouvelle lune, de la vitesse de la Lune dans un repère héliocentrique . En 2020 il y a 13 pleines lunes.
Le déplacement rétrograde de la ligne, en gris, des nœuds de l'orbite lunaire les fera coïncider avec la nouvelle lune vers le 20 juin et le 15 décembre ce qui donnera lieu aux deux éclipses de Soleil de l'année.

Vénus en 2020

 Vénus montre ses phases de mars à octobre.

la rencontre Mercure-Vénus de fin mai

A la fin du mois de mai, de jour en jour, Vénus descend vers l'horizon le soir. Concurremment Mercure apparait et s'élève. La rencontre a lieu le 22 mai au soir. 
Pour un lieu de latitude 46° N et de longitude 7° E, vers 21h30, une demi-heure après le coucher du soleil, les deux astres sont à 10° de hauteur et le soleil à 5° sous l'horizon. La magnitude de Mercure atteint -0.3.
Il y a là une bonne opportunité de repérer Mercure très près de l'immanquable Vénus.

La conjonction de Vénus se produit au nœud descendant le 3 juin.

 

Après les transits de juin 2004 et juin 2012, la conjonction de juin 2020 échappe au soleil

Le prochain transit se produira au nœud ascendant 105,5 années après celui de juin 2012, en décembre 2117.

La latitude négative de la planète dès le 4 juin retarde sa réapparition comme étoile du matin.

la Lune, les planètes, les nœuds de l'orbite lunaire en 2020

 La figure ci-dessus montre le déplacement relatif des planètes sur l'écliptique représenté par le segment horizontal.
Les périodes favorables à l'observation de Mercure, en fonction de l'angle de l'écliptique avec l'horizon, apparaissent en pointillé gras:

le soir première décade de février et du 15 mai au 15 juin,

le matin: du 15 juillet à début août et mois de novembre.

Pendant la journée du 18 mars, les planètes Mars, Jupiter et Saturne reçoivent, dans cet ordre, la visite du croissant de la Lune éclairée à 30%. Cette concentration peu habituelle est visible de 5h à midi.

Sur la figure, on constate que le Soleil rencontre le nœud ascendant de l'orbite lunaire vers le 20 juin et le nœud descendant vers le 15 décembre. Deux éclipses de soleil se produisent donc lors des nouvelles lunes voisines de ces deux dates.

Les ÉCLIPSES en 2020

Cette année compte six éclipses, ce qui est peu courant: une éclipse de lune le 10 janvier, un triplet d'éclipses: de lune le 5 juin, de soleil le 21 juin et de lune le 5 juillet, et enfin un couple d'éclipses, de lune le 30 novembre et de soleil le 14 décembre.

Le Soleil était passé le 30 décembre 2019 au nœud descendant et il atteint le nœud ascendant le 19 juin 2020 puis, de nouveau, le nœud descendant le 11 décembre.

La nouvelle lune du 26 décembre 2019 avait éclipsé le Soleil à proximité du nœud descendant et la pleine lune du 10 janvier 2020 se produit 20 heures après son passage au nœud ascendant. En conséquence sa latitude est élevée (1.1°) et la Lune échappe à l'ombre de la Terre. Il s'agit d'une forte éclipse mais par la seule pénombre. C'est la dernière de la série courte d'éclipses de Lune au nœud ascendant commencée en février 2017.

Le triplet de juin/juillet correspond à un chevauchement de série courte d'éclipses de Lune au nœud descendant: l'éclipse du 5 juin est la première d'une nouvelle série de quatre, celle du 5 juillet la dernière de la série courte précédente! Ce phénomène de chevauchement reproduit celui du triplet constaté en juillet/août 2018 pour les séries courtes d'éclipses de soleil au nœud ascendant.
Les deux éclipses de Lune sont donc faibles, ce sont des éclipses par la pénombre.

21 juin 2020 6h41, la Lune et la Terre éclipsée vues du Soleil

vue cavalière

21 juin éclipse annulaire en Asie

La nouvelle lune du 21 juin se produit à 6h41 TU, peu après son passage au nœud ascendant (3h), l'éclipse est donc forte et concerne l'hémisphère nord et l'Asie. Elle est annulaire. C'est le numéro 3 de la série courte d'éclipses de Soleil au nœud ascendant commencée en juillet 2018 dont les éclipses se déplacent du sud au nord.

L'éclipse de Lune du 30 novembre inaugure une nouvelle série courte au nœud ascendant: elle se produit bien avant le nœud (22h), elle est forte mais par la pénombre seulement.

14 décembre 2020 16h17, la Lune et la Terre éclipsée vues du Soleil

vue cavalière

14 décembre éclipse totale pour le Pacifique et l'Atlantique sud

La nouvelle lune du 14 décembre se produit à 16h17, peu après le nœud descendant (6h) : l'éclipse est forte et concerne l'hémisphère sud (Amérique du sud et océans Pacifique et Atlantique). C'est une éclipse totale. C'est le numéro 3 de la série courte d'éclipses de Soleil au nœud descendant commencée en janvier 2019 dont les éclipses se déplacent du nord au sud.

2020 année BISSEXTILE

Après de multiples errements durant des siècles, c'est en l'an 708 de la fondation de Rome, que Jules César adopte la réforme recommandée par l'astronome Sosigéne d'Alexandrie: il fixe la date du 25 mars pour l’équinoxe, arrête la règle du doublement du sixième jour avant les calendes du mois de mars, une fois tous les quatre ans, et fait commencer l'année au 1er janvier au lieu du 1er mars. Le premier janvier de départ correspond au 01/01/45 avant JC. L'année civile compte donc 365 + 1 / 4 jours.
Mais la règle est mal appliquée pendant plus de trente ans. C'est sous Auguste, fils adoptif de César, que la correction intervient. En réalité la réforme julienne n'est respectée qu'à partir de l'an 5 après JC. Dix ans plus tard, le Sénat Romain, en hommage à ces réformateurs baptise le 5ème mois, devenu le 7ème, julius (juillet) et le 6éme, devenu huitième, augustus (août).
Mais l'année tropique entre deux équinoxes successifs compte en réalité 365.24219879... jours.
Une dérive s'installe donc, et le concile de Nicée en 325, sans comprendre les raisons du décalage, en prend acte et entérine la date du 21 mars pour l'équinoxe.
Mais la dérive s'amplifie et le concile de Trente en 1562 charge le pape Grégoire XIII de résoudre la question. Les savants de l'époque savent que l'année compte 365 + 97 / 400 jours et, pour réduire l'année civile de 3 jours sur 400 ans, ils recommandent de supprimer à l'avenir le caractère bissextile des années séculaires sauf celles dont le millésime est divisible par 400.

L'année civile compte alors 365 + 1 / 4 - 1 / 100 + 1 / 400 jours, soit 365.2425 jours. L'écart est ramené à 26 secondes par an.


Le 24 février 1582 une bulle papale décrète le nouveau calcul des années bissextiles et, pour ramener l'équinoxe au 21 mars, supprime 10 jours à l'année 1582: le lendemain du jeudi 4 octobre sera le vendredi 15!

Mais il s'agit là d'une réforme catholique acceptée avec retard par les pays des autres religions.

Kepler: "Les protestants aiment mieux être en désaccord avec le soleil qu'en accord avec le pape".

(notice largement inspirée de l'ouvrage "Calendriers et chronologie" de J.P. Parisot et F. Suagher, Masson éditeur 1977)