|
| reconstitution Jlert Joseph Lertola wikipedia |
 |
| wikipedia |
Cet article est un complément à celui publié le 16 juillet 2014 et intitulé: "Stonehenge Decoded". En effet le passage du Nœud ascendant de l'orbite lunaire au Point Gamma au début de l'année 2025 donne l'occasion de préciser le fonctionnement du modèle en privilégiant l'observation des levers et couchers des Pleines Lunes.
Le cercle Aubrey compte 56 trous. Ce nombre 56 est presque un diviseur commun des vitesses des cinq astres acteurs des éclipses et il permet facilement de concrétiser leurs positions respectives au cours de l'année. En effet 56 * 0.5 = 28 nombre très proche de la révolution sidérale de la Lune, 27.32 j, 56 * 6.5 = 364 j nombre très proche des 365.25 j de l'année et 56 * 121 = 6776 j nombre très proche des 6800 j de la révolution en 18.61 ans des nœuds.
Les pieux représentant le Soleil, et l'Ombre, symétriques autour de la Terre au centre du monument, sont déplacés d'un trou, alternativement après six jours et après sept jours. Le pieu représentant la Lune est déplacé de deux trous par jour et d'un trou supplémentaire tous les 20 jours. Ceux représentant les Nœuds, symétriques, sont déplacés d'un trou tous les 121 jours, en sens inverse car leur marche se fait dans le sens rétrograde.
Dans l'étude qui suit, la Terre, au centre, figure en bleu clair, le Soleil en jaune, l'Ombre de la Terre en gris clair, la Lune en jaune clair et les Nœuds en rouge. Les pieux tournent dans le sens est/sud/ouest (comme le Soleil de son lever à son coucher) sauf ceux des nœuds. La numérotation des 56 trous commence à celui qui correspond à l'équinoxe de printemps, jour facile à déterminer car lors de celui-ci l'ombre de l'extrémité d'un piquet vertical décrit une ligne droite de l'est à l'ouest. Ce pieu-origine se trouve sur l'axe d'accès au monument.
Les éclipses se produisent lors des pleines ou nouvelles Lunes à condition que celles-ci interviennent près des Nœuds car alors le Soleil doit franchir la zone pendant laquelle il est voisin de l'orbite lunaire ce qui peut déclencher son occultation par la nouvelle Lune ou celle de la pleine Lune par l'Ombre de la Terre.
Compte tenu des dimensions des orbites et des diamètres apparents des astres concernés, les saisons d’éclipses centrées sur les nœuds s'étendent sur 18 jours de part et d'autre ce qui correspond à un peu moins de trois pieux: 2.8. Par prudence ces saisons agrandies à six trous figurent en un arc de cercle rouge autour de chaque nœud.
L'acteur principal des éclipses est évidemment le Soleil et il n'y a éclipse que quand celui-ci s'aventure dans l'une ou l'autre saison d'éclipses ce qui se produit deux fois par an avec une avance de 11 jours d'une année sur la précédente puisque 12 lunaisons valent 354.4 jours, si la condition de voisinage du nœud est suffisamment remplie.
Une éclipse de Lune est visible depuis la moitié du globe opposée au Soleil: il suffit de tourner son regard vers elle entre soir et matin. Elle dure entre 5 et 6 heures, c'est donc un phénomène observable en un lieu donné environ une fois par an.
Par contre lors d'une éclipse de Soleil, une partie seulement de la Terre est plongée dans l'ombre de la Lune. En moyenne au cours de l'éclipse, à un instant donné, la zone de visibilité correspond à l'intersection avec la Terre du cône d'ombre de rayon double de celui de la Lune soit environ le quart de la surface terrestre. Cette zone se déplace sur la Terre du fait de sa rotation sur elle-même à 500 m/s à l'équateur, et du déplacement dans le même sens de la Lune à 1 km/s. La durée de l'éclipse peut atteindre 3 heures. Dans cette zone seule une très petite part, la zone de centralité, 2% seulement, connait une obscuration complète du disque solaire. Mais un Soleil amputé de 98% de son disque reste assez lumineux pour qu'un promeneur ne se doute de rien et ne décèle pas le phénomène extraordinaire de la Lune qui, à 400'000 km, passe lentement devant le Soleil 400 fois plus loin.
Par contre, un "sachant" peut facilement mettre en évidence l'éclipse par réflexion sur une surface liquide ou par le principe de la chambre noire percée d'un trou minuscule qui fait apparaitre sur son fond l'image de la source lumineuse ou encore en attirant l'attention sur l'aspect des images du Soleil passant au travers du feuillage serré des arbres.
Une éclipse partielle de Soleil peut ainsi être vue en moyenne une fois tous les deux ans et demi en un lieu donné.
A Stonehenge, au cours de l'année 2025, le 14 mars, la Lune, éclipsée par la pénombre à partir de 4 h, se couche totalement éclipsée par l'ombre de la Terre à 6h à l'ouest. Le 29 mars le Soleil est partiellement éclipsé pour un tiers par la Lune à partir de 10h et jusqu'à midi avec un maximum à 10h47.
Le 7 septembre la Lune totalement éclipsée se lève à 18h30 à l'est puis sort de l'ombre et échappe à la pénombre à 21h. Par contre l'éclipse de Soleil du 21 septembre n'est pas visible car l'axe Soleil / Lune passe au delà du pôle sud. L'éclipse concerne seulement le pacifique sud...
Le score s'établit pour 2025 à trois éclipses visibles sur quatre!
Mais compte tenu de ce que les vitesses des astres ne sont pas exactement divisées par le nombre 56 il va se produire à la longue un décalage.
Pour y remédier, des alignements comportant buttes de surélévation et pierres de visée ont été construits. Le monument comporte deux buttes notées 92 et 94 et deux pierres notées 91 et 93, disposées
aux quatre coins d'un rectangle quasiment inscrit dans le cercle Aubrey. La diagonale de ce rectangle joignant les deux pierres 91 et 93 fait un angle de 60° avec la
direction nord/sud et représente donc les azimuts
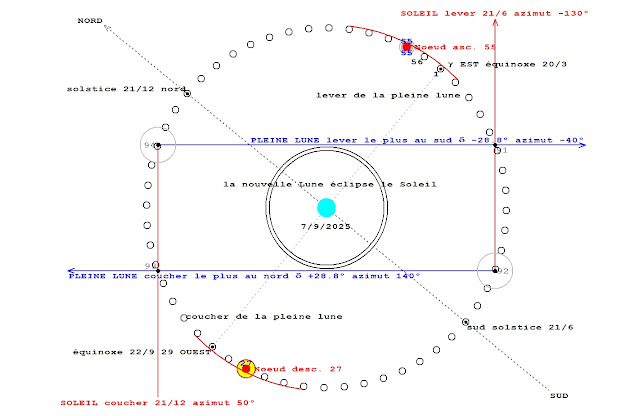
-60° et +120°. L'autre diagonale joignant les deux buttes 92 et 94 fait un angle de 20° avec la direction nord/sud et représente donc les azimuts -20° et 160°. Le grand coté du rectangle représente les azimuts -40° et +140°, le petit coté les azimuts -130° et +50°.
On verra ci-dessous que les dimensions respectives des cotés de ce rectangle, leur rapport est de 2.75, n'ont rien d'anodin car elles résultent des règles qui commandent les nœuds de l'orbite lunaire.
En un lieu de latitude (la) l'azimut (A) du lever et du coucher d'un astre, mesuré depuis le sud, ne dépend que de sa déclinaison (d) par la formule A = arccos(-sin(d)/cos(la)).
Lors des solstices, le Soleil présente sa déclinaison maximale de +/- 23.5°, valeur admise pour l'époque, -4'000 ans, de la construction du monument. La latitude de Stonehenge étant de 51.2°, les azimuts de son lever et de son coucher valent alors arccos(-sin(+/-23.5)/cos(51.2)), c'est à dire -130 / 50°: ce sont les directions des petits cotés du rectangle et des alignements de la butte 92 vers la pierre 91 en été et de la butte 94 vers la pierre 93 en hiver.
A l'occasion des solstices (Soleil aux trous 15 et 43), on peut donc ajuster éventuellement, la position du pieu du Soleil. Pour ce faire on surveille en été le lever du Soleil en visant, à partir de la butte 92, la pierre 91 et en hiver le coucher du Soleil en visant, à partir de la butte 94, la pierre 93.
La position du Soleil étant ajustée, celle de la Lune en découle lors de la prochaine pleine Lune.
Pour les Nœuds la procédure d'ajustage se complique car ils sont invisibles et ceci alors que leur position est capitale pour la prévision des éclipses.
Mais un observateur attentif de la Lune peut remarquer qu'il y a des années lors desquelles les Pleines Lunes de l'hiver sont très hautes dans le ciel et que celles de l'été restent très basses sur l'horizon. Il ne s'agit pas d'un caprice de la Lune comme semble le laisser penser le nouveau rédacteur des Éphémérides édités par la SAF, mais bien de la conséquence du phénomène appelé "nutation" dû aux interactions des forces de gravitation entre Soleil, Terre et Lune.
C'est le cas des années 2024 et 2025.
Le nœud ascendant de l'orbite lunaire passe au point gamma au début janvier 2025. Sur la figure ci-dessus, pour l'année 2025, on a dessiné depuis la butte 92 une flèche dans la direction correspondant à chacun des couchers des douze Pleines Lunes et depuis la butte 94 dans la direction correspondant à chacun de leurs levers. On a fait figurer la date de ces couchers et levers avec la valeur de la déclinaison de la Lune à ces instants.
Le fonctionnement du modèle est en effet basé sur l'observation des azimuts des levers et couchers des Pleines Lunes.
L'orbite lunaire coupe l'écliptique en deux nœuds, là où ont lieu les éclipses, mais elle coupe aussi l'équateur en deux autres nœuds, appelons-les: nœuds équatoriaux. Ceux-ci oscillent autour des points de l’écliptique correspondant aux équinoxes: le Point Gamma, pour le printemps, et son symétrique. L'amplitude est voisine de 13 degrés et la période est celle des nœuds: 18.61 années. L'effet de la nutation n'est pas moindre qu'un balancement de l'axe de rotation de la Terre, le pôle nord décrivant une ellipse de demi-axes d'environ 9 et 7 secondes d'arc: voilà, en plus des marées, une véritable influence lunaire. La nutation fut découverte et nommée par l'astronome britannique James Bradley (1693/1762) en 1745 après l'observation durant vingt années de l'étoile gamma du Dragon. Elle fut expliquée par le mathématicien français et Homme des Lumières Jean d'Alembert (1717/1783).
La Lune décrit son orbite dans un plan qui fait un angle variant entre 5.0° et 5.3° par rapport au plan de l'écliptique où se trouve le Soleil. Ce dernier plan faisait, au moment de la création du monument il y a 4'000 ans, un angle de 23.5° par rapport à l'équateur. Lorsque le Nœud équatorial passe au Point Gamma, le Nœud ascendant de l'orbite lunaire est confondu avec eux et la déclinaison d'un point de l'orbite lunaire résulte alors de l'addition des deux obliquités en valeur absolue et varie alors entre le maximum de 23.5° + 5.3° soit 28.8° et le minimum de -23.5° -5.3° soit -28.8°. La déclinaison de la Pleine Lune peut donc atteindre ce maximum en valeur absolue quand le Soleil se trouve près des solstices.
De la même façon, lorsque c'est le nœud descendant qui se trouve au Point Gamma la déclinaison d'un point de l'orbite varie entre les valeurs 23.5° - 5.3° soit 18.2° et -23.5° + 5.3° soit - 18.2°.
Au voisinage du solstice d'hiver la déclinaison du Soleil vaut -23.5° et donc la déclinaison de la Pleine Lune qui lui est opposée peut atteindre son maximum de 28.8°: la Pleine Lune est haute dans le ciel et au voisinage du solstice d'été, quand la déclinaison du Soleil vaut +23.5°, celle de la Pleine Lune peut être voisine de -28.8°: la pleine Lune est basse sur l'horizon.
Il y a donc un lien direct entre la déclinaison maximale de la Pleine Lune et la proximité entre Point Gamma et Nœud ascendant ou descendant.
En conséquence la surveillance de l'azimut des levers et couchers de la Pleine Lune
renseigne sur sa déclinaison et donc sur l'écart entre les nœuds
équatoriaux de l'orbite et le point gamma. Lorsque l'azimut maximal du
coucher (ou lever) de la Pleine Lune est atteint le nœud ascendant
coïncide avec le point gamma. Si cet azimut reste cantonné à des valeurs qui résultent des déclinaisons de +/- 18.2° c'est le nœud descendant qui
coïncide avec le point gamma.
On peut ainsi procéder à l'ajustement des positions des nœuds. Bien entendu, ce contrôle ne peut intervenir qu'une fois tous les 9.3 ans soit tous les 3800 jours...
Les azimuts des levers et couchers des Pleines Lunes lors de la déclinaison maximale de +/- 28.8° valent arccos(-sin(28.8)/cos(51.2)) soit 140 ° et -40°. Ce sont précisément les directions des grands cotés du rectangle et des alignements depuis la butte 92 vers la pierre 93 en hiver et depuis la butte 94 vers la pierre 91 en été.
Les azimuts des levers et couchers du Soleil et la Pleine Lune, lorsqu'ils sont à leur maximum de déclinaison, sont donc deux à deux perpendiculaires. La raison réside dans la valeur de la latitude: dans un lieu d'une autre latitude il ne s'agirait que d'un parallélogramme. Cette valeur X est la racine de l'équation arccos(-sin(23.5)/cos(X)) + arccos(23.5+5.3)/cos(X)) = 270. Par dichotomie on obtient 51.3° ce qui est bien, à 0.1° près, la latitude de Stonehenge.
Pour l'autre déclinaison maximale de la Lune, +/- 18.2°, cet azimut vaut arccos(-sin(18.2)/cos(51.2)) soit 120° et -60° qui sont les directions de la diagonale des pierres 91 et 93. Les visées faites depuis la pierre 91 vers la pierre 93 correspondent aux couchers et dans l'autre sens aux levers. C'est cette circonstance qui décide de l'implantation de la pierre 91 à l'azimut 60°: voir ci-dessous le rectangle"magique"...
On peut noter que ces azimuts visés depuis les buttes coupent les directions des levers et couchers du Soleil lors des solstices en deux points particuliers. Pour le lever de la Pleine Lune, il s'agit du point symétrique de la butte 92 par rapport à la pierre 91 et pour le coucher, du point symétrique de la butte 94 par rapport à la pierre 93. Ces nouveaux points sont-ils marqués sur place par des pierres qui seraient utilisées si la vue directe à travers le centre n'est plus possible.
Il convient de noter que les pierres suspendues en linteau et leurs piliers qui occupent la partie centrale n'ont été érigés que plusieurs centaines d'années postérieurement à la phase I du monument qui date des années 2'000 BC.
C'est au début du mois de juin 2036 que le nœud descendant passera au point gamma. La déclinaison de la Lune ne sera alors jamais supérieure, en valeur absolue, à 18.2°.
Début août 2043 ce sera au tour du nœud ascendant de repasser au point gamma, reproduisant alors une figure analogue à celle du 9 janvier 2025 plus haut.
 |
| un rectangle "magique"? |
Les constructeurs de Stonehenge n'avaient nul besoin de connaissances ou de considérations d'ordre scientifique. Ils n'étaient pas des proto-astronomes mais des hommes curieux et intelligents, observateurs avertis, qui avaient fait le lien entre les Pleines ou Nouvelles Lunes et le Soleil pour expliquer les éclipses. La gestion rigoureuse du site devait leur permettre de prédire la plupart de ces phénomènes stupéfiants s'il en est.
Le choix du site ne s'est pas fait au hasard et doit résulter d'essais antérieurs jusqu'à l'obtention d'une figure simple. Stonehenge devait ainsi jouir d'une aura particulière et d'un statut "pontifical"!