Le Panorama des étoiles

la tête de veau par "Night Star" (c 1985)

Représenter une demi sphère céleste complète sur un plan? Une gageure impossible!

La projection stéréographique de l'astrolabe de l'Antiquité et du Moyen Age déforme les constellations jusqu'à ne plus pouvoir les reconnaître. C'est principalement un outil de calcul réservé à des initiés. La carte classique d'aujourd'hui, dite "équidistante azimutale", centrée sur le pôle nord concentre dans son ovale rotatif les étoiles coté nord et dilate l'espacement de celles du sud. Elle reste malaisée à consulter car l'utilisateur comprend mal la façon de l'orienter et se trouve dérouté dans son maniement. Son avantage essentiel réside dans la facilité, relative, de son réglage pour l'adapter au ciel du jour mais la latitude du lieu d'observation est fixe.

Il existe des projections qui peuvent présenter plus ou moins fidèlement l'ensemble de la moitié du ciel qui se trouve devant l'observateur. La Société Astronomique de France publie ainsi chaque mois dans sa revue mensuelle L'astronomie, "l'aspect du ciel à la latitude de Paris le 1er du mois vers 21h15 ou le 16 vers 20h15", pour les horizons sud et nord. Mais ces instants horaires donnés sans explication sont curieusement uniformes tout au long de l'année sans égard pour la variation de la déclinaison du Soleil. La longitude du lieu retenu n'est pas précisée et son influence est passée sous silence alors que l'écart de l'heure solaire entre Brest 4.49° O et Strasbourg 7.75° E atteint presque 50 minutes, deux codes non identifiés affectent la couleur et le diamètre des étoiles. L'espace libre loge la légende d'autres figures...

On peut mieux faire pour une présentation du ciel étoilé originale et remarquablement parlante!

Quelques prolégomènes

 

le jour et l'heure

"Hommes de peu de foi, ne trouvez-vous pas merveilleux que la Terre tourne sur elle-même en vingt-quatre heures tout juste?" cité in "Le Calendrier", PUF, par l'astronome français et membre de l'Union rationaliste, Paul Couderc (1899/1981).

Les Chaldéens qui vivaient au IX ème siècle av. J.C. dans le sud de la Mésopotamie divisaient le jour en soixante parties, peut-être parce que ce nombre est le PPCM de 2, 3, 4 et 5. Chaque partie du jour était elle-même divisée en soixantièmes. Plus tard les Babyloniens ont utilisé une division du jour en douze parties, plus simple d'emploi au seul prix de l'abandon de la qualité de multiple de 5. Le nombre 12 revêtirait d'ailleurs un caractère "sacré" (?) puisqu'en outre, en moyenne deux fois sur trois, l'année compte 12 lunaisons.

La numération à base soixante demeure en vigueur aujourd'hui pour les minutes et les secondes: elle a traversé les siècles bien qu'elle ne soit pas adaptée au calcul de la durée entre deux instants. Elle s'est naturellement propagée à la mesure des angles (aussi en raison des "presque" 360 jours de l'année...), ainsi qu'à la mesure des distances en mer et dans les airs, le mille marin étant la longueur de l'arc de l'équateur terrestre sous-tendu par un angle égal à une minute d'arc. Cette unité de longueur, internationalement utilisée, découle de la définition du mètre proposée par les savants des Lumières (un mille mesure 10'000'000 / (90*60) = 1851.85 m.).

Les Hébreux, après leur captivité à Babylone au VIII ème siècle av. J.C., reprirent cette division du jour en douze parties, mais en l'appliquant à la journée et à la nuit: le jour compte alors 24 "heures". Les Grecs puis les Romains conservèrent cet usage devenu plus tard quasiment universel.

Mais il y a eu une certaine variété pour l'origine du décompte: midi, minuit, lever du soleil, coucher du Soleil et même division de la nuit (et de la journée) en douze heures de durée "temporaire"!

Les horloges astronomiques médiévales dérivées de l'astrolabe de l'Antiquité comportent un cadran de deux fois 12 heures avec une seule aiguille faisant un tour par jour car il s'agissait de représenter le modèle d'un système solaire géo-centré. En Italie, dans la province du Latium, les horloges équipant les édifices publics d'avant le XIX ème siècle présentent un cadran de 6 heures avec une seule aiguille faisant quatre tours par jour: il s'agit là d'une numération à base 6 ! Les cadrans modernes ont un cadran mixte de 12 heures et de 60 minutes avec deux aiguilles, celle des heures faisant deux tours par jour et celle des minutes tournant 12 fois plus vite. Le lecteur est censé savoir faire le partage entre les deux moitiés du jour: c'est une numération à base 12. Une fois sur cinq les graduations coïncident ce qui conforte la numération à base soixante pour les minutes et confirme la fécondité du nombre 12. Les anglo-saxons retiennent une numération des heures en 12 valeurs avant ou après midi au lieu de 24 valeurs à partir de 0h...vestige du cadran médiéval ?

 

primatiale Saint Jean à Lyon

Le Quirinal, résidence du Président de la République Italienne

clocher à Tolentino

60 = 12 * 5

Les astronomes d'aujourd'hui utilisent une échelle universelle de date et d'heure basée sur "l'ère julienne" et retiennent une division décimale du jour. Cette échelle, qui n'a pas de rapport direct avec Jules César, a été élaborée par le chronologiste français huguenot Joseph Scaliger (1540/1609) en 1583, un an après la réforme du calendrier par le pape Grégoire XIII (1502/1585), pape à la conduite un peu hors normes et maître du temps...En prenant en compte les cycles de la Lune, de la semaine et de variables utilisées pour le comput ecclésiastique de la date de Pâques (toujours en vigueur!), il en a fixé le début au lundi 1er janvier de l'année bissextile 4713 av. J.C. à midi (il n'y a pas d'année zéro). Le jour julien commence ainsi à midi, au méridien de Greenwich.

L'instant du 1er août 2023 à 14h TU est désigné par le nombre 2'460'158.08333...Les astronomes ne se laissent pas rebuter par les nombres astronomiques!

Les Révolutionnaires Français ont voulu, en 1792, soumettre le calendrier à un ordre républicain et décimal et s'ils conservèrent douze mois - Lune oblige - mais de trente jours chacun, ils les divisèrent en trois décades. Le jour comprenait dix heures de cent minutes, soit 1'000 minutes au lieu de 1440. A 5 heures il était midi! Ce calendrier ne parvint pas à s'imposer et ne résista pas à l'Empire et au retour du pouvoir ecclésial: le 11 nivôse an XIV redevint le 1er janvier 1806. Le grade pour la mesure des angles, 400 grades pour 360 degrés, a mieux résisté en France mais sans s'imposer car non multiple de trois.

rarissime cadran solaire républicain (musée de Boston), source Sky & Telescope

le temps sidéral

D'un jour au jour suivant, les étoiles, pour faire un tour en un an, se décalent dans le ciel d'une fraction de degré très proche de l'unité puisque l'année dure 365.2422 jours: 360 / 365.2422 = 0.985°. Chaque nuit elles avancent donc vers l'ouest dans le ciel visible: elles se lèvent et se couchent environ quatre minutes plus tôt. En un mois elles se décalent de 30° et en quinze jours de 15°.

La Terre tourne sur elle-même en 24 heures soit 15° par heure.

Il en résulte que 15 jours après avoir contemplé le ciel nocturne, un observateur peut voir les étoiles presqu'à la même place s'il s'y prend une heure plus tôt: les étoiles se seront décalées d'à peu près 15° mais la rotation incomplète de la Terre sur elle-même aura compensé ce décalage. Une carte du ciel établie pour le 1er du mois à l'heure H est aussi valable pour le 16 du mois à l'heure H-1!

C'est un peu la magie des 12 lunaisons et des 24 heures: 24 demi-mois correspondent à 24 heures.

Pendant qu'il regarde les étoiles, l'observateur humain se déplace dans l'espace puisqu'il est embarqué sur un vaisseau spatial qui, non seulement tourne sur lui-même autour de la direction du pôle nord en 24 heures, mais aussi se déplace sur une orbite autour d'un point "fixe", le Soleil, dans un plan qualifié d'écliptique qui fait un angle de 23.438° avec cette direction. Cette orbite coupe le plan de l'équateur céleste perpendiculaire à la direction du pôle en deux points correspondant aux équinoxes, là où nuit et journée ont une durée égale. Celui du printemps, appelé point vernal sert d'origine pour les coordonnées célestes. On le désigne aussi par point gamma, cette lettre grecque étant le symbole de la constellation du bélier qui l'hébergeait  du temps de l'astronome égyptien Claude Ptolémée (100/168).

Les astronomes ont choisi pour caractériser, à un instant donné et en un lieu donné, la position de la Terre sur son orbite, la valeur de l'angle entre le méridien Sud et le point vernal, c'est à dire l'angle horaire de ce point. Au cours d'un jour cet angle passe de 0° à 360°: il correspond à la marche quotidienne d'environ 0.985° de la Terre. Le point vernal étant fixe et la Terre progressant, il atteint la valeur de 360° un peu avant qu'il se soit écoulé 24 heures sur la Terre. Chaque jour, à la même heure, il progresse de 0.985°. Mais il est mesuré en heures et non pas en degrés, comme les ascensions droites, et a malencontreusement reçu en France le nom de "temps sidéral", l'adjectif sidéral rappelant qu'il s'agit d'une notion astrale. Il vaudrait mieux parler comme les anglo-saxons d'angle horaire sidéral.

temps sidéral

 En un an la Terre fait 365.2422 tours sur elle-même et aussi un tour autour du Soleil. Par rapport au point vernal elle fait donc un tour de plus sur elle-même, soit 366.2522 tours . Ce tour supplémentaire est fractionné en autant de jours de l'année comme indiqué plus haut. Le temps nécessaire chaque jour pour que le temps sidéral passe de 0 à 360° est donc en moyenne égal à 366.2422 / 365.2422 soit 0.99727 jour, d'où un écart de 0.00273 jour, soit 3 minutes et 56.555 secondes par jour. Le "jour sidéral", mieux dénommé la "révolution sidérale", dure donc 23 heures, 56 minutes et 4.09 secondes de temps.

C'est par abus scriptural que l'on peut lire: "24 heures sidérales équivalent à 23h 56m 4.09s".

Voir l'article du présent blog en date du21/01/2015 intitulé "le cadran de temps sidéral"

A 15 jours d'intervalle, au même instant, le temps sidéral se trouve augmenté en moyenne de 15 fois 3minutes et 55.91secondes soit 59 minutes, c'est à dire, à très peu près, une heure. En quinze jours moins une heure, la différence de temps sidéral n'est plus que d'une minute et, à un quart de degré près, les étoiles sont à la même place dans le ciel vu depuis la Terre.

 

la projection des étoiles

Le problème quoique classique n'est pas simple: il s'agit de réduire un quart de sphère en un demi-disque!

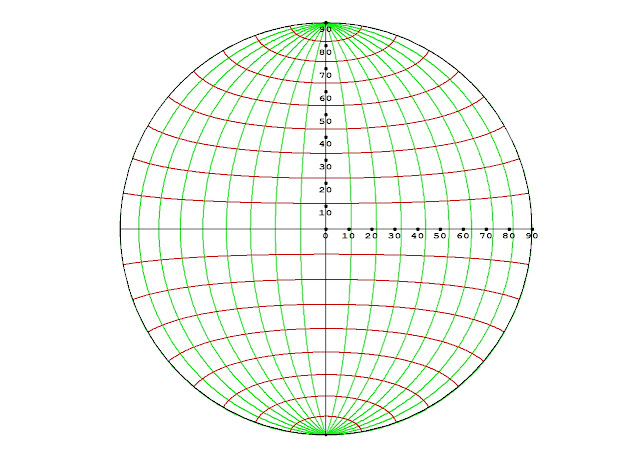
En 1701 Philippe de La Hire (1640/1718), mathématicien et astronome français, a imaginé pour la conception d'un astrolabe universel, c'est à dire utilisable à toutes les latitudes, une projection d'une demi-sphère sur un plan méridien qui remédie sensiblement aux défauts de ceux de ses prédécesseurs. Dans cette projection les méridiens et les parallèles célestes deviennent des arcs d'ellipse. Sur le contour de l'astrolabe, les étoiles se trouvent légèrement relevées mais sans trop altérer la forme reconnaissable des constellations car cette projection est presque "équivalente".

Elle permet de représenter une moitié du ciel visible centrée vers une direction quelconque. Les panoramas en demi-disque obtenus montrent l'ensemble des constellations de la moitié du ciel qui fait face à l'observateur, sur 180°, de l'horizon au zénith: c'est presque une photographie grand angle!

En l'espèce cette projection s'avère un meilleur compromis que la projection azimutale équivalente de Lambert qui respecte moins les azimuts. Johan Heinrich Lambert (1728/1777), mathématicien et philosophe né à Mulhouse, a notamment laissé son nom à deux systèmes de projection cartographique encore utilisés de nos jours.

voir l'article du présent blog en date du 27/01/2023 intitulé "une mystérieuse carte du ciel"

 

les panoramas mensuels valables pour le 1er du mois et 16 du mois

S'agissant de représenter le ciel étoilé, l'instant retenu pour établir les panoramas est l'heure à laquelle, le 16 de chaque mois, les principales étoiles deviennent visibles, le Soleil se trouvant alors à environ 12 ou 13 degrés sous l'horizon. Cette heure est éminemment variable. L'heure d'été est prise en compte.

On peut présenter deux versions des panoramas mensuels. L'une mentionne l'équateur céleste en pointillé bleu, l'écliptique en rouge, la voie lactée en pointillé noir gras et les étoiles, sans les astres dont la position varie dans le temps: différente chaque mois, elle est permanente d'une année à la suivante.

L'autre version mentionne en plus, pour le moment précisé, les positions du Soleil, de la Lune, des planètes et des nœuds de l'orbite lunaire qui déterminent les éclipses et qui avancent de 18.63 jours par an et les dates de passage du Soleil à ces nœuds. Figurent aussi l'image fidèle de la Lune, son orbite en pointillé gris fin et sa course dans le ciel en pointillé gris gras. Les heures de lever et de coucher de la Lune pour le 1er du mois et pour le 16 sont indiquées avec mention de sa fraction éclairée ce qui permet de savoir si elle gêne les observations. Les dates des pleines et nouvelles lunes du mois sont précisées ainsi qu'éventuellement, celles des éclipses et leur visibilité. Quelques renseignements d'ordre astronomique figurent comme, par exemple, l'heure au Soleil pour permettre de caler une carte céleste du commerce. Cette version doit être recalculée pour chaque mois.

SUD

NORD

EST

OUEST

Ne pas oublier que le lever de la Lune en pleine nuit , s'il éteint les étoiles, est un spectacle saisissant:

" Dans le ciel, les étoiles se levaient tour à tour parmi les coupoles ou les aiguilles des montagnes. La Lune n'était point d'abord à l'horizon, mais son aube s'épanouit par degrés devant elle, de même que ces gloires argentées dont les peintres du XIVème siècle entouraient la tête de la Vierge: elle parut enfin...sur la crête dentelée du Fourquela..." Chateaubriand (1768/18448), Mémoires d'outre tombe (P. IV, L. 2, ch. 14).

Dans l'ultime paragraphe de cette œuvre rédigé à Paris au mois de novembre 1841 l'auteur écrit:

" Il est 6 h du matin. J'aperçois la Lune pâle et élargie; elle s'abaisse sur la flèche des Invalides à peine révélée par le premier rayon doré de l'Orient..."

Une telle description du ciel, habituellement fidèle de la part de l'auteur, a conduit le Directeur de l'Observatoire de Paris, André Danjon (1890/1967), "chateaubriandiste" fervent, à subodorer une mauvaise lecture du manuscrit par le copiste car elle se révèle incompatible avec la date du 16 novembre 1841 comme indiqué dans les éditions habituelles. Tous calculs faits, André Danjon penche pour la véritable date du 1er novembre, au petit matin, peu avant le coucher de la Lune, la mention "er" ayant été prise pour un "6" ? (Maurice Levaillant, Édition du centenaire, 1948)...

Chateaubriand par Anne Louis Girodet

l'heure légale

Au temps des cadrans solaires chaque lieu avait son heure et il était midi quand le Soleil atteignait sa culmination, au moment où l'ombre portée du "style" était la plus courte. Avec l'accélération des moyens de transport il a fallu harmoniser l'heure d'un certain territoire. On a finalement partagé le globe terrestre en 24 fuseaux horaires de 15 degrés chacun et l'heure du milieu du fuseau s'est imposée, avec des aménagements, à tout lieu compris dans ce fuseau.

Les étoiles sont restées bien entendu étrangères à ces conventions...Si on veut donc ajuster une carte céleste "équidistante azimutale" du commerce à l'aspect réel du ciel pour un instant donné, il faut tenir compte de l'écart de longitude entre le lieu d'observation et le centre du fuseau légal. L'heure légale européenne est celle du fuseau +1h par rapport au temps universel de Greenwich, et celle du fuseau +2h en été. Le méridien central du fuseau +1h passe un peu à l'ouest de Vienne (16° est). Sa limite occidentale (7.5° est) passe sensiblement par Bâle, Berne et Evolène: géographiquement la Suisse Romande appartient au fuseau zéro.

A Sion ou Arbaz de longitude 7.38 est, la correction du temps des étoiles par rapport au temps légal s'établit à 15° - 7.38° soit 7.62° ou 30 minutes et 28 secondes, et 1 heure 30 minutes et 28 secondes en été.

En été, quand il est midi à Sion, le Soleil est plein sud à Kiev (30° 31' est) et les valaisans doivent encore attendre une heure et demi pour voir le Soleil à son plus haut...

fuseaux 0, 1, 2

 

Deux autres ajustements améliorent la précision de ce genre de carte céleste . Le premier, très simple, tient à la place de l'année en cours dans le cycle quadriennal de la bissextilité (0.25 jour par an).

Le second consiste en la prise en compte de la variation de la position du pôle nord parmi les étoiles. En effet sa direction. inclinée de 23.438° sur l'écliptique, subit une rotation en 25'800 ans autour de celle du pôle de l'écliptique. Ce phénomène est dû aux forces gravitationnelles exercées par la Lune et le Soleil sur le bourrelet équatorial de la Terre, lui-même généré par sa rotation. C'est la précession des équinoxes: le point vernal se présente chaque année en avance car il se déplace sur l'écliptique d'un angle 50.3 secondes d'arc par an. Depuis le début de l'astronomie il a parcouru un peu moins de 30°, soit environ un signe du zodiaque.

Ce phénomène modifie les deux coordonnées équatoriales, ascension droite et déclinaison, de tous les astres et rend leur calcul précis extrêmement complexe. Certains éditeurs de cartes célestes (Hallwag pour la carte Sirius) fournissent des tabelles - assez absconses - pour calculer une fraction de jour à prendre en compte, mais avec quelle fiabilité?

Ephémérides graphiques trimestiels 2023 pour le Valais central (Suisse)

EPHEMERIDES GRAPHIQUES DÉTAILLES 2023

premier trimestre

 Mercure est visible le matin lors de la deuxième quinzaine de janvier.

deuxième trimestre

Pas de chance: éclipse de Soleil alors qu'il n'est pas encore levé et de Lune qui se termine lors de son lever. Mercure est visible le soir, la première  quinzaine d'avril.

troisième trimestre

 Vénus fait sa boucle au mois d'août (la conjonction se produit le 13), elle est alors au plus près de la Terre. Saturne est à l'opposition fin août: elle se lève quand le Soleil se couche.

quatrième trimestre

En octobre, éclipse de Soleil alors qu'il est déjà couché et très petite éclipse de Lune vers 22h15 heure d'été. Mercure se montre le matin début octobre. Le 9 novembre la Lune et Vénus se lèvent ensemble vers 3h et,entre 11h et midi, le croissant de lune occulte Vénus. Jupiter est à l'opposition début novembre: elle se lève quand le soleil se couche.

On constate une symétrie autour de la fin juin entre les trimestres (1er et 4ème d'une part et 2ème et 3ème d'autre part). La déclinaison de la Lune est alors voisine de zéro vers minuit.

LUNISTICE

En 2023 les déclinaisons extrêmes de la Lune sont importantes et dépassent, en valeur absolue, la valeur de 28°. En effet on se rapproche du "lunistice" de la Lune qui interviendra au début du mois de février 2025 quand le nœud ascendant de l'orbite lunaire sera aligné avec le point vernal ( point gamma). Les nœuds sont animés d'un mouvement rétrograde assez irrégulier qui leur fait faire un tour en 18.60 ans et il en découle que, tous les 18 ans et 7 mois environ, l'inclinaison de l'orbite lunaire qui varie entre 5° et 5.3° s'ajoute à celle de l'écliptique, 23.44°. Le maximum de la valeur absolue atteint donc 28.7°. La Lune peut alors être très basse et très haute dans le ciel.

Lunistice de début 2025: la déclinaison de la Lune atteint son maximum de 28.7°

 

Lorsque c'est le nœud descendant qui est aligné avec le point vernal il se produit l'inverse: la déclinaison de la Lune peut atteindre un minimum égal à l'écart entre 23.44° et 5° soit 18.4° en valeur absolue, c'est ce qui s'est passé à la mi-novembre 2015, 9 ans et 3 mois avant le lunistice de 2025.

LEVERS ET COUCHERS de la LUNE

Les fortes valeurs de la déclinaison lunaire entraînent un écart important pour la durée du transit dans le ciel: le 2 novembre, avec la déclinaison de +28°, la Lune se lève à 20h21 et se couche le lendemain à 12h33 soit un transit de 16h11m. Quatorze jours plus tard, le 16 novembre, avec la déclinaison de -28°, elle se lève à 11h14 et se couche à 18h56 soit un transit de 7h41m égal à 48% de celui du 2 novembre. A l'issue de la lunaison entamée le 2, le 29 novembre, la Lune retrouve une déclinaison de +28°, elle se lève à 18h7 et se couche le lendemain à 10h18 soit un transit de 16h11m analogue à celui du début de lunaison. Les 9 et 23 novembre la déclinaison s'annule et le transit dure 12heures.

heures des levers et couchers lors de la demi-lunaison du 2 au 16 novembre

 

heures des levers et couchers de la demi-lunaison du 16 au 29 novembre

 

Chacune des figures ci-dessus représente sur une horloge en 24 heures les instants des levers, en rouge, et des couchers, en bleu, durant une demi lunaison moyenne.

Pour une déclinaison décroissante, du 2 au 16, les levers successifs sont espacés et les couchers successifs serrés et inversement en déclinaison croissante du 16 au 29. L'axe de symétrie correspond aux dates pour lesquelles la déclinaison s'annule, les 9 et 23 novembre.

La révolution synodique, c'est à dire par rapport à un méridien donné de la Terre, dure 29.53 jours. Deux passages consécutifs de la Lune à ce méridien sont donc séparés par une durée moyenne de 24h50m29s. Chaque jour la Lune "avance" donc dans le ciel, vers l'est, d'un peu plus de 50 minutes. Son rythme ne s'accorde pas à celui du Soleil. Ceci explique qu'à la cadence de 29.5 jours il n'y a pas de lever de Lune et pas de coucher : la Lune est encore dans le jour d'avant ou déjà dans celui d'après. En novembre 2023, le 6 il n'y a pas de lever et le 20 pas de coucher. 

La rapidité de l'évolution de la déclinaison de la Lune est responsable de la forme en "S" de la succession des levers - et des couchers - de la Lune. Cette forme s'accentue pour les latitudes élevées en valeur absolue, l'angle horaire H étant donné par la formule cos(H) = -tan(lat)tan(dec) où lat représente la latitude du lieu et dec la déclinaison de la Lune.

L'article du présent blog en date du 20/07/2021 intitulé "éphémérides graphiques et quelques considérations lunaires" présente, in fine, l'explication géométrique de ces variations.

lever de Lune peu après l'éclipse du 05/05/2023

Le lever héliaque de Sirius

 

SIRIUS la bellissime

 

Pendant la journée, l’atmosphère terrestre diffuse la lumière issue du Soleil et empêche de discerner les étoiles de la voûte céleste qui sont cependant bien présentes. Du fait de la rotation de la Terre autour du Soleil les étoiles composant cette voûte changent: tout se passe comme si, d'un jour à l'autre, le Soleil se déplaçait vers l'est d'environ un degré par rapport aux étoiles qui, elles, resteraient fixes.

Par ailleurs, en raison de l'inclinaison de l'axe de la Terre sur son orbite, depuis un lieu donné, par exemple en Valais central (Suisse), les étoiles se classent en trois catégories: celles toujours visibles car suffisamment proches du pôle nord (déclinaison supérieure à 43.7°), celles toujours invisibles car trop proches du pôle sud (déclinaison inférieures à -46.3°)et, entre les deux, celles qui, au fur et à mesure de l'écoulement des jours, composent chaque soir un ciel étoilé différent.

Au cours de l'année, une étoile observable est visible si elle se lève avant le Soleil ou se couche après lui et la durée de son absence dépend de la latitude du lieu et de ses coordonnées célestes, ascension droite et déclinaison.

On désigne par lever héliaque (du grec helios: soleil) d'une étoile l'instant où, pour la première fois après une absence plus ou moins longue, elle réapparait à l'est, à la fin de la nuit juste avant que la lueur du Soleil levant ne vienne l'éteindre. A ce moment l'étoile se situe à environ 2° au-dessus de l'horizon est et le Soleil 7° en-dessous. Par la suite, elle se lève et se couche de plus en plus tôt, un certain jour elle se lève deux fois à 23h56m d'écart et devient étoile du soir puis, un autre jour elle se couche deux fois et redevient étoile du matin, enfin, à partir de son coucher héliaque, elle n'est plus visible. Les jours doublés correspondent à la différence entre temps solaire et temps sidéral (celui des étoiles): 24 heures de temps solaire équivalent à 23h56m4s de temps sidéral puisque par rapport au Soleil, en un jour, la Terre tourne plus qu'une étoile d'une quantité égale à 1/365.25 de tour.

La déesse Sothis (Sirius) wikipedia

 

Les Égyptiens avaient choisi comme jour de l'an celui du lever héliaque de Sirius (ou Sothis), étoile principale de la constellation du Grand Chien dans l'hémisphère sud céleste, la plus brillante du ciel et divinisée à ce titre. A partir de ce jour le Soleil consent, au bout de plusieurs mois d'appropriation à rendre aux hommes la contemplation de la plus belle étoile! L'évènement, facile à détecter dans le désert, coïncidait avec l'arrivée des fortes chaleurs de la canicule, "période du Chien", et annonçait la survenance de la crue du Nil si importante pour l'agriculture.

Après un peu plus de 40 siècles, cette date proche originellement du solstice d'été se trouve retardée d'environ 60 jours en raison de la "précession (i.e. avancée) des équinoxes" due à la lente rotation de l'axe de  de la Terre par rapport à l'axe de son orbite. Cette rotation est engendrée par les forces de gravitation exercées par le Soleil et la Lune sur le renflement équatorial de la Terre. De nos jours, pour l'annonce de la saison des fortes chaleurs il faut retenir le lever héliaque d'Aldébaran, principale étoile du Taureau.

En Valais central (Suisse), le 19 août à 5h55, le lever héliaque de Sirius s'observe à l'azimut -63°

 

En Valais, le lever héliaque de Sirius se produit le 19 août à 5h55, heure d'été, au sud/sud-est (azimut 63° est), mais son observation est réservée aux alpinistes postés à 3.800 m d'altitude! (Le Mont Fort semble un peu bas...). Le Soleil se lève une demi-heure plus tard à l'est/nord-est (azimut 110° est).

Le coucher héliaque intervient le 11 mai à 21h33 au sud/sud-ouest (azimut 63° ouest). Sirius reste donc invisible 100 jours par an du 12 mai au18 août. Sa conjonction avec le Soleil a lieu le 2 juillet.

Du 25 novembre au 1er février elle resplendit dans le ciel d'hiver depuis son lever jusqu'à son coucher durant 9h34m. Son opposition avec le Soleil a lieu le 1er janvier. Étoile de l'hémisphère sud, sa déclinaison négative de -16°44'41" fait qu'elle n'est jamais très haute dans le ciel du Valais: elle culmine à 27° de hauteur.

Sirius présente un alignement très remarquable avec les trois rois du baudrier d'Orion puis Aldébaran du Taureau et enfin les Pléiades. Avec Rigel, Aldébaran, Capella, Castor, Pollux et Procyon elle forme un polygone concentrant des étoiles parmi les plus belles du ciel.

Sirius a inspiré Voltaire (1694/1778) pour établir les critiques portées par les philosophes des Lumières à l'encontre de la Société du XVIII ème siècle: son célèbre personnage du conte philosophique paru en 1752, Micromégas, est originaire d'une planète de l'étoile Sirius... Ce géant entreprend une visite critique et humoristique de la Terre après escale sur Saturne et Jupiter. Sur sa route il est passé près de Mars et a côtoyé les deux lunes signalées en 1727 (!) par Gulliver (Jonathan Swift 1667/1745)... Phobos et Deimos seront découverts par Asaph Hall (1829/1907) en 1877!

Sirius et la métaphore "du point de vue de Sirius" ont été pris comme emblèmes par Hubert Beuve-Méry (1902/1989), fondateur en décembre 1944, à l'instigation du Général De Gaulle, du journal "Le Monde", sur les ruines du journal "Le Temps" accusé de collaboration.

Nouveau Micromégas, il a signé "Sirius" un billet quasi-quotidien publié pendant 25 ans (et a proscrit toute photographie dans son journal) jusqu'à sa retraite prise en 1969, quelques mois après la démission du Président De Gaulle devenu son adversaire de plume...

Une mystérieuse carte du ciel?

Camille Flammarion (1842/1925), vulgarisateur scientifique enflammé, crée en 1882 la revue mensuelle "L'Astronomie" et fonde en 1887 la

Société Astronomique de France. (SAF)

 

 "N'est-il pas étrange que les habitants de notre planète aient presque tous vécu jusqu'ici sans savoir où ils sont et sans se douter des merveilles de l'univers?"

médaille SAF célébrant la nuit (NOX)

  

Il publie en 1879 un volume de près de 900 pages intitulé "L'Astronomie Populaire". Il s'agit d'une œuvre de vulgarisation à destination du grand public qui synthétise et modernise les quatre volumes du cours d'astronomie donné par François Arago (1786/1853) à l'Observatoire de Paris. Ce livre connait un immense succès: 130.000 exemplaires de 1879 à 1924.

 

 

En page 5 le livre présente une allégorie de la Terre emportée par le Temps et il s'achève par la publication de l'abjuration extorquée en juin 1633 à Galilée (1564/1642) par le tribunal de l'Inquisition.

"L'Astronomie" a fêté ses cent quarante ans l'année dernière. Depuis 1973, au moins (date de l'adhésion de l'auteur de ces lignes), et jusqu'au début des années 2000, chaque numéro mensuel incluait "le ciel du mois", deux cartes du ciel en forme de demi cercle dessinées par Lucien Tartois et présentant l'aspect du ciel étoilé au dessus de l'horizon sud et de l'horizon nord de Paris.

A partir du numéro 117 de novembre/décembre 2003, la publication des éphémérides du mois a repris et les cartes semi circulaires ont retrouvé leur place après un "coup de jeune".

Pour les amateurs ces deux cartes mensuelles figurent parmi les fleurons de la la SAF car, sauf erreur, on ne les trouve nulle part ailleurs, alors que leur usage est d'une simplicité biblique: nulle complication pour les orienter, nul besoin de les tourner ni de les brandir au dessus de sa tête: ce sont... les cartes Michelin du ciel!

Mais quelle projection est-elle utilisée pour les établir? La SAF, interrogée, n'est pas formelle et parle d'une projection azimutale de Lambert version Schmidt.

 

Adrien Germain (1837/1895) entre à l’École Polytechnique à 19 ans en 1856 puis intègre le Corps des Ingénieurs Hydrographes de la Marine. En 1866 il fait paraître une somme intitulée "Traité des projections des cartes géographiques Représentation plane de la sphère et du sphéroïde".

Il reçoit en récompense deux ans plus tard la médaille d'or de la Société de Géographie. Ce traité de près de 400 pages incluant des dizaines de planches, recense et décrit plusieurs dizaines de projections.

 

Dessiner sur un plan une surface sphérique impose de renoncer soit à la représentation exacte des angles soit à l'exactitude des surfaces. L'application emblématique du premier choix est l'astrolabe  de la haute antiquité et sa projection stéréographique, celle du second, la carte médiévale de Mercator (1512/1594) et ses latitudes croissantes.

 

 Alors que la vogue de l'astrolabe a déjà grandement décru, un mathématicien français, géographe et cartographe, Philippe de La Hire (1640/1718), s'est penché, le premier, sur la recherche d'un compromis entre ces deux écueils. Parmi ses nombreuses occupations La Hire s'est affirmé comme le continuateur de Desargues (1591/1661) et de Pascal (1623/1662) au sujet des coniques, il a participé à la géodésie de la France, a laissé son nom à un mécanisme transformant un mouvement circulaire en mouvement linéaire...

 

le "rétrécissement" de la France de Louis XIV par ses astronomes dont La Hire

CNAM "théorème" de La Hire

La Hire, plus géographe qu'astrolabiste, s'intéresse aux projections d'une demi sphère à partir d'un point de l'un de ses diamètres sur un plan perpendiculaire à ce diamètre au centre de la sphère.

Une telle projection, avec pour point de vue un point sur la sphère, la projection stéréographique, a été retenue au moyen âge par l'astronome andalou Arzaquiel (1029/1087) pour construire un astrolabe universel c'est à dire fonctionnant à toutes les latitudes (cf la somme "L'Astrolabe" de Raymond D'Hollander 1999). Les méridiens et parallèles sont des cercles. Il y a un resserrement vers le centre de la projection car l'espacement des méridiens est fonction de l'azimut A par la fonction tan(A/2).

En 1551, l'espagnol Juan Rojas (XVI siècle) s'intéresse à la question en plaçant le point de vue à l'infini, la projection devenant alors orthographique. Les méridiens sont des ellipses centrées sur la projection du point de vue et les parallèles des segments. Mais il se produit une dilatation encore plus gênante car l'espacement est fonction de l'azimut A par la fonction tan((pi/2-A)/2).

 

 

In medio stat virtus, a du pensé La Hire...en plaçant le point de vue dans une position intermédiaire.

 

Pour une sphère dont le rayon est pris pour unité, d représentant la distance entre son centre et le point origine de la projection, les coordonnées de la projection de l’étoile de hauteur H et d'azimut A sont:

abscisse: d*sin(A)cos(H) / (d+cos(A)cos(H))

ordonnée: d*sin(H) / (d+cos(A)cos(H))

principe de la projection de La Hire

les méridiens et les parallèles sont des parties d'ellipses excentrées

 

la projection de La Hire

Sur les axes (H =0 ou A=0) la fonction donnant l'abscisse sur l'horizon est identique à celle donnant l'ordonnée sur la verticale:  V = d*sin(U) / (d+cos(U)). Il y a donc symétrie sur les axes.

 

Cette relation liant U et V reste très proche de la linéarité pour des valeurs de d comprises entre 1.68 et 1.75. Il en découle qu'entre ces valeurs l'espacement est presque régulier: un peu diminué pour les faibles valeurs de la variable et un peu augmenté pour les fortes valeurs, les proportions restant limitées à quelques pourcents.

 

La Hire s'est fixé comme critère de choix pour la distance entre l’œil et le centre, que, sur l'horizon, la projection du méridien d'azimut 45° soit au milieu de celles du méridien 0° et du méridien 90°. Il en découle géométriquement que cette distance doit être égale à 1 + rac(2) / 2, soit 1.7071.

Ce choix, particulièrement simple, se révèle pertinent puisque l'écart entre l'espacement réel des méridiens (et donc aussi des parallèles) ne diffère que de moins de 0.5° d'un espacement régulier (en retenant la valeur 1.677, on pourrait réduire un peu cet écart).

L'espacement entre méridiens et entre parallèles est quasiment régulier

 

La Hire présente ce nouvel astrolabe universel à l'académie des sciences le 3 décembre 1701.

 

Jean Henri Lambert est né à Mulhouse en 1728, 10 ans après le décès de La Hire, et il est mort en 1777 à 49 ans à Berlin. C'est un précurseur des nouvelles mathématiques: nombres complexes, fonctions hyperboliques...et de la philosophie des sciences. Il a exercé son art, notamment, dans le domaine de la cartographie où il a laissé son nom à des projections toujours utilisées deux siècles et demi plus tard: la projection zénithale équivalente et les projections conique et cylindrique conformes.

 

Lambert a découvert que, pour obtenir une projection de la sphère sur un plan qui respecte les surfaces (projection équivalente), il faut considérer le grand cercle qui passe par le pôle de projection et le point à projeter et retenir la valeur r de la corde du pôle à celui-ci. Si A est son azimut on a donc r = 2*sin(A/2).

la projection zénithale équivalente de Lambert

 

Si on choisit comme point central, un point de l'équateur, la trigonométrie sphérique montre alors que les formules à retenir (Germain opus cité, page 324) pour les coordonnées polaires (r,t) de la projection dans ce repère, d'un point de latitude H et de longitude A sont les suivantes:

 

r = rac(2)sin(u/2) où u est donné par cos(u)=cos(A)cos(H)

t = arctan(tan(H) / sin(A))

 

la projection de Lambert

Le résultat de cette projection ressemble étonnamment à celui de la projection de La Hire. Une partie de l'explication tient au fait que dans les deux projections l'angle polaire d'un point projeté est identique: dans les deux cas la tangente de cet angle s'écrit sin(H) / (sin(A)cos (H)).

Chez Lambert le rayon s'exprime par r = rac(2)sin(u/2) où u est donné par cos(u) = cos(A)cos(H). Chez La Hire le rayon peut également être exprimé en fonction de la variable u. Tous calculs faits on établit la relation r = 1.707*sin(u) / (1.707+cos(u)). Nous avons vu plus haut que cette relation reste très proche de la linéarité entre 0 et pi/2, r restant équivalent à la fonction r = 2u / pi alors que chez Lambert elle a l'aspect d'une sinusoïde très amortie dont le développement limité r = rac(2)*(u/2-u^3/48+u^5/3840...) reste proche de la fonction précédente.

Chez Lambert le point projeté se trouve toujours plus éloigné du centre que chez La Hire.

pente unique pour les deux projections, Lambert en bleu et La Hire en rouge

 

projections comparées La Hire en rouge et Lambert en bleu

 

 

La projection de Lambert conserve les surfaces mais induit une distorsion dans la position des étoiles ce qui modifie un peu l'aspect des constellations. Aux environs de 60° de hauteur une étoile est repoussée vers le haut et pour 60° d'azimut elle se trouve décalée vers les bords est ou ouest.

La projection de La Hire donne donc une représentation et un agencement plus fidèles des constellations.

 

On peut remarquer qu'une certaine projection de type La Hire se rapproche beaucoup de la projection de Lambert. En effet en retenant pour la distance du point de vue la valeur de 2.26 au lieu de 1.7071, on obtient la figure ci-dessous qui rassemble les deux projections:

projection de Lambert en bleu et projection type La Hire pour un œil à 2.26 en rouge

 

La courbe représentant la relation V = 2.26*sin(U) / (2.26+cos(U) met en évidence la distorsion induite par la représentation de Lambert:

en bleu: distorsion induite dans la valeur de l'azimut par la projection de Lambert

La distorsion trouve son maximum, 3.8°, entre 50° et 65° d'azimut ou de hauteur.

le ciel du Valais central en projection de La Hire

le ciel du Valais central en projection de Lambert

 Il apparait que la projection de La Hire pourrait être préférée.

 

 

Si on choisit comme point central de la projection un lieu quelconque de la Terre de latitude la, Adrien Germain (opus cité page 325) donne les coordonnées polaires (r,t) de la projection d'un point de latitude H et de longitude A: 

r = rac(2)sin(u/2) où u est donné par cos(u) = sin(H+phi)sin(la) / cos(phi)

phi, angle auxiliaire, étant lui-même donné par tan(phi) = cos(A) / tan(la)

cos(t) = sin(A)cos(H) / sin(u)

 

On obtient une carte de la Terre particulièrement esthétique: