2016: transit de mercure etc... voici le programme!

Mercure est la grande vedette de 2016 en traversant le soleil en mai.

Vénus se cache presque toute l'année.

Mars est constamment présent et s'approche très près en mai.

Jupiter et Saturne se montrent le matin puis le soir jusqu'en août.

Le soleil et la lune ont rendez-vous en mars et septembre... mais plutôt dans les mers chaudes.

L'ombre de la terre assombrit la lune 15 jours après ces rendez-vous mais à la marge.

Le transit de MERCURE

mercure autour du soleil en 2016, le 9 mai, terre, mercure et soleil sont alignés

le phénomène astronomique vu dans le plan de l'écliptique

En Valais (CH) le lundi 9 mai à 13h12, le soleil est au sud, 15 minutes avant son plus haut dans le ciel suisse. Mercure aborde le disque du soleil par l'est. C'est une très petite tache noire: son diamètre n'est que 0.64% de celui du soleil. Au fur et à mesure de la course du soleil, il décrit une courbe en "S" qui est la trace de la projection de la planète sur le plan du disque solaire. A 16h56, il est au plus près du centre du soleil qui est alors au sud ouest à une hauteur de 38.4°.
Ce n'est qu'à 20h40 que le soleil peut se débarrasser de cet intrus, par le sud, quelques minutes avant son coucher.
L'affaire a duré 7h30m.
Elle se reproduira le 11 novembre 2019, au nœud ascendant et non plus descendant et les deux premiers tiers du transit seront seuls visibles avant le coucher du soleil.
Des explications complémentaires sont disponibles dans l'article du présent blog en date du 14 août 2014 intitulé "voir mercure et mourir..."

le phénomène vu de la terre (Valais CH)

Quid des autres planètes? 

le parcours des planètes sur leurs orbites en 2016 

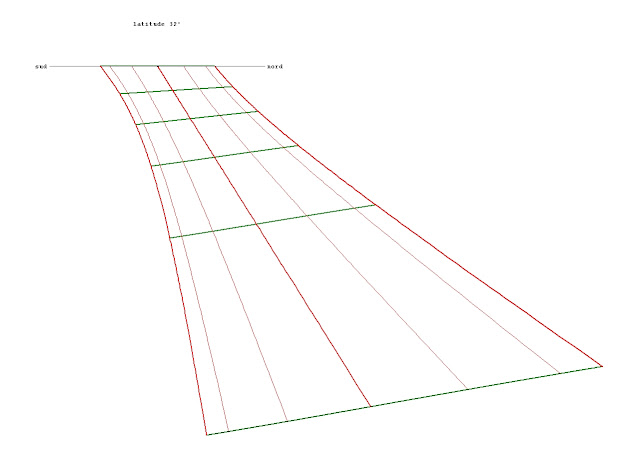
La marche des cinq planètes est représentée dans la figure ci dessous où le segment horizontal est l'écliptique, le soleil étant au milieu.

vue d'ensemble des positions relatives sur l'écliptique du soleil, des planètes et de la lune en 2016

On constate que mercure (ligne grise) s'écarte sensiblement du soleil à sept reprises (cinq fois seulement avec profit pour les observateurs), que vénus (ligne noire) reste assez près du soleil de février à octobre, que mars (ligne rouge), au contraire, en est toujours éloigné, que jupiter (ligne bleue) est du matin en début et en fin d'année et du soir de mars à août, et que saturne (ligne verte) commence l'année le matin, la continue le soir puis disparait en novembre.

Vénus et saturne se rapprochent le 9 janvier et le 30 octobre, mars et saturne font route commune de mars à septembre et sont au plus près le 25 août.

Les lignes pointillées des dragons (nœuds de l'orbite lunaire) coupent la ligne verticale noire du soleil le 12 mars et le 4 septembre: ce sont les dates auxquelles le soleil se trouve à ces nœuds. Les éclipses de soleil se produisent les 9 mars et 1er septembre.

Les planètes, qui sont toutes du matin en février, sont toutes du soir en août.

En début d'année, en Valais vers 7h30 le matin, la lune visite les cinq planètes: jupiter le 28 janvier, mars le 1er février, saturne le 3 puis vénus et mercure ensemble le 6. 
 

début février la lune en l'espace de 8 jours rend visite aux cinq planètes

Le 27 août, vénus et jupiter sont  très proches l'une de l'autre et mercure n'est pas loin. A 14h57 les trois planètes sont presqu'alignées dans la direction du sud. Il est alors facile de trouver les deux planètes brillantes... et d'imaginer mercure.

 

fin août, rapprochement de jupiter, vénus et mercure

La chasse à mercure en 2016

Au tout début de l'année, le soir, et depuis une semaine déjà, mercure, assez haut dans le ciel, est visible au sud ouest, une demi heure après le coucher du soleil. Il est à la quadrature le 1er janvier.

le 1er janvier au soir, mercure assez haut sur l'horizon

  
A la fin janvier mercure est du matin, assez haut dans le ciel, au sud est, une demi heure avant le lever du soleil. Il est à la quadrature le 2 février.

fin janvier le matin

Dès le 4 avril, le soir, mercure fait une remontée fulgurante puis une descente analogue qui se termine le 27 avril. A la mi avril, le soir, mercure est au plus haut, à l'ouest, à près de 18° au dessus du soleil. Il est à la quadrature le 16 avril.

mercure, le soir du 17 avril au plus haut

A la fin de septembre, le matin, mercure, à l'est, se hisse à 17° au dessus du soleil avec une importante magnitude de -0.3. Il est à la quadrature le 29 septembre. Ce jour-là il reçoit la visite d'un très fin croissant de vieille lune.

29 septembre au matin: mercure et la lune

Le 11 octobre au matin mercure et jupiter sont très proches. Mercure a une belle magnitude de -0.9 car il est assez éloigné du soleil à 1.26 UA, celle de jupiter est de -1.3.

11 octobre au matin, mercure et jupiter au plus près

En fin d'année aux environs du 15 décembre le soir mercure fait une belle apparition. Il est à la quadrature le 14 décembre.

mi décembre le soir, mercure, vénus et mars de conserve.

Vénus en 2016

En début d'année Vénus, très belle étoile du matin, poursuit sa descente sur l'horizon entamée en octobre 2015, elle est très proche de saturne le 9 janvier et disparait fin février.

la plongée de vénus étoile du matin

 
Vénus se montre à nouveau à partir de début octobre comme étoile du soir et entame alors une vigoureuse remontée qui ne cessera que début février 2017.

la réapparition de vénus, le soir, proche de saturne début novembre

 Vénus passe 7 mois avec Apollon, à l'opposé de la terre!

Terre, soleil et vénus sont alignés du 5 au 7 juin et durant ces 3 jours le soleil éclipse la planète qui, précisément, passe au nœud ascendant de son orbite le 7 juin. A cet instant les centres des 3 astres sont quasiment alignés!

7 juin, vénus, soleil et terre presqu'exactement alignés

Mars en 2016

Si vénus boude les terriens ce n'est pas le cas de mars qui est visible toute l'année, d'abord le matin puis le soir.

Le 22 mai, mars est à l'opposition et se trouve le 31 mai à 0.50 UA de la terre avec un diamètre apparent de 18.6", loin du record de l'opposition d'août 2003 (25.1"), mais mieux que lors de la précédente opposition d'avril 2014 (15.8"). 
Les prochaines missions vers mars devront quitter la terre au début de février 2016 pour une arrivée sur mars début octobre.

missions pour mars en 2016

Les départs suivants utiliseront l'opposition du 27 juillet 2018 et auront lieu en mai 2018 pour une arrivée en janvier 2019.
Pour plus d'explications voir l'article du présent blog de mai 2014 intitulé "les huit planètes du système solaire" in fine.

Jupiter, d'abord splendide astre du matin, passe à l'opposition le 8 mars. Astre du soir ensuite, elle resplendit tout l'été puis reste près du soleil en septembre et octobre (conjonction le 25 septembre) pour réapparaitre le matin en novembre et décembre.
Il en est de même, avec un décalage de quelques 3 mois, pour saturne qui passe à l'opposition le 3 juin et disparait à la mi novembre (conjonction le 10 décembre).

Deux éclipses de soleil et deux éclipses de lune en 2016

Les nœuds de l'orbite lunaire coïncident cette année avec la position où se trouve le soleil le 12 mars pour le nœud descendant et le 4 septembre pour le nœud ascendant. Les dragons se tiennent en embuscade à ces deux dates et le soleil ne peut les approcher sans être éclipsé par la lune. Compte tenu de la rétrogradation des nœuds ce n'est pas six mois qui les séparent mais seulement 173.3 jours en moyenne. Mais en 2016 l'écart entre le 12 mars et le 4 septembre est de 176 jours parce qu'entre ces deux dates la terre décrit une bonne partie de la portion de son orbite (du 4 avril au 4 octobre) où elle est la moins rapide, l'aphélie se produisant le 4 juillet.

L'éclipse de soleil au nœud descendant commence le 9 mars à 0h19 et n'est donc visible qu'aux antipodes de l'Europe. Elle se produit alors que la lune est toute proche de son périgée, à 360.000 km de la terre. Il en résulte que cette éclipse est totale et que dans la bande de centralité la durée de l'occultation du soleil est particulièrement importante.
Cette éclipse porte le numéro 2 de la suite courte d'éclipses au nœud descendant qui a commencé avec celle du 20 mars 2015. Elle se produit avant le nœud et concerne donc plutôt l’hémisphère nord.

Pour plus d'explications voir l'article du présent blog de février 2015 intitulé "éclipses de soleil en série".
 

9 mars 2016: éclipse peu avant le nœud descendant

l'éclipse à l'instant de son maximum, vue du soleil

carte de l'éclipse

L'éclipse est visible en Asie du sud est.

l'éclipse à l'instant de la nouvelle lune 1h54 UTC

L'éclipse de soleil au nœud ascendant se produit le 1er septembre alors que la lune se trouve assez près de son apogée (392.000 km de la terre) elle est donc annulaire. Cette éclipse porte le numéro 2 de la suite courte d'éclipses au nœud ascendant qui a commencé avec celle de septembre 2015. Elle se produit avant le nœud et concerne donc l'hémisphère sud.

1er septembre 2016: éclipse peu avant le nœud ascendant

 La longueur du cône d'ombre est insuffisante pour qu'il atteigne la terre!

l'éclipse à l'instant de son maximum, vue du soleil

carte de l'éclipse

L'éclipse est visible en Afrique centrale du Gabon à Madagascar.

l'éclipse à l'instant de la nouvelle lune 9h3 UTC

Les deux éclipses de lune de mars et septembre 2016 ne sont que des éclipses par la pénombre et seule celle du 16 septembre est visible en Europe.

éclipse de la lune par la pénombre le 16 septembre 2016

Ce jour-là, en Valais (CH), la lune se lève à l'est déjà partiellement éclipsée à 19h43. A l'instant de la pleine lune, 20h5, elle se trouve à l'ouest sud ouest et à 15° de hauteur.

Claude Mellan graveur

 Merveilleuse allégorie mise en scène par Pietro da Cortona (1596-1669) pour orner un livre du botaniste Giovanni Battista Ferrari (1584-1655) et gravée par l'artiste français Claude Mellan (1598-1688): la déesse Séléné conduit son char dans le ciel nocturne alors que Nyx, déesse de la nuit noire, se protège de son éclat à l'aide d'un voile. Séléné désigne les constellations de la balance et du scorpion et indique ainsi à la déesse Flore que l'heure est venue de planter les fleurs à bulbe. Quatre putti assistent les personnages (exposition Mellan, musée Jenisch Vevey CH).

Le Traité de l'Analemme, par Ptolémée

Claude Ptolémée (90-168) vivait à Alexandrie. Son nom dérive du lieu de sa naissance, Ptolémaïs près de Thèbes en Haute Égypte.
Il était de citoyenneté romaine car depuis les suicides de Marc-Antoine et Cléopâtre consécutifs au désastre de leur armée à Actium, en -31, face à Octave (le futur empereur Auguste), l’Égypte est romaine.
Mais ses origines sont gréco-égyptiennes puisque Cléopâtre était la dernière représentante de la dynastie des Ptolémée qui remontait au partage de l'empire d'Alexandre Le Grand, proclamé pharaon en -331.

Ses écrits astronomiques, dont le Traité de l'Analemme, sont rédigés en grec.
L'Analemme, ici, n'a aucun lien autre que l'homonymie avec la célèbre courbe en huit.
 
La librairie Blanchard à Paris diffuse un ouvrage édité en 2009 par les Editions Bergeret à Mérignac intitulé "Claude Ptolémée Livre de L'Analemme". Il s'agit d'une traduction du latin en français par Jean Peyroux (1925-2012), ingénieur des Arts et Métiers, d'un texte publié en 1562 à Rome par Frédéric Commandin, mathématicien italien. Cet ouvrage est remarquable et on cite ici le début de l' "avertissement du traducteur":

" Le texte grec de Claude Ptolémée ne nous est pas parvenu. Au XVI ème siècle, l'italien Frédéric Commandin, ayant découvert un manuscrit latin ayant pour titre Analemme de Claude Ptolémée, décida de le publier. Ce manuscrit latin est une mauvaise traduction, d'ailleurs incomplète, de manuscrits arabes du texte grec qui ont disparu. Le traité latin, avec des figures obscures et compliquées, fut complété et commenté par Commandin souvent peu clair lui aussi."

Dès 1817 Delambre (1749-1822), astronome et mathématicien français, avait analysé sans concession le livre de Commandin dans son Histoire de l'Astronomie Ancienne. Ces deux ouvrages permettent de reconstituer la science gnomonique des Grecs (et de faire litière des approximations émises sur l'Analemme de Ptolémée).

Il apparait que l'Analemme n'est autre qu'un traité justifiant et explicitant la marche à suivre pour la construction géométrique, sur un cadran solaire disposé dans un plan horizontal ou vertical plein sud ou vertical plein est, du point d'ombre portée par le sommet du gnomon (tige perpendiculaire au plan du cadran).
Le traité se terminait par des tables numériques donnant les valeurs à retenir pour les principaux "climats", pour le début de chaque signe du zodiaque et pour chaque heure. Ces tables permettaient ainsi de tracer rapidement des cadrans solaires dont la précision quoique relative était suffisante. Elles ont toutes disparu sauf celle correspondant au commencement du signe du Cancer pour le climat de 13h.

Il faut préciser que le cadran solaire à style polaire parallèle à l'axe du monde n'existait pas encore du temps des Grecs et que les heures courantes étaient des heures dites temporaires car égales à la douzième partie de la durée variable entre lever et coucher du soleil. Quant à la notion de "climat", il s'agit d'une façon de chiffrer la latitude par la durée en un lieu, en heures équinoxiales (égales), du temps séparant lever et coucher du soleil le jour du solstice d'été. Ainsi le climat de 13h correspond à la latitude de 16.5° pour une obliquité chiffrée à 23.83° par Ptolémée.

Ptolémée repère la position du soleil à un instant donné par 3 grands cercles qui, pour deux d'entre eux, ne sont pas ceux utilisés de nos jours, mais qui se révèlent très judicieux pour les cadrans solaires. Ces 3 cercles sont le "cercle de descente" qui passe par le zénith et le nadir (pour nous le vertical de l'astre), le "cercle horaire" qui passe par les points nord et sud (rien à voir avec le nôtre) et le "cercle hectémorion" qui passe par les points est et ouest.

les trois grands cercles de Ptolémée et les trois arcs à mesurer

Ptolémée a mis au point une méthode employant règle et compas pour représenter la valeur des arcs de grand cercle séparant l'astre du zénith en bleu (notre angle à l'astre), du point sud en rouge et du point est en vert. Il emploie une projection orthographique selon la direction est ouest sur le plan du méridien et procède à un rabattement sur ce plan du chemin suivi par le soleil pendant la journée.

en jaune la course du soleil depuis son lever jusqu'à midi, en rouge son rabattement sur le plan méridien

L'arc en bleu est le cercle horaire au sens moderne. Le soleil "S" se projette en "s" et se rabat en "S' ". La longueur du segment sS', égale par construction à celle du segment sS joue un rôle essentiel dans la suite.
La mathématique des Anciens Grecs ne connaissait pas les chiffres d'aujourd'hui: on utilisait les lettres de l'alphabet. Leur trigonométrie ne connaissait pas les lignes trigonométriques modernes: on utilisait la seule notion de "corde" qui est, dans un cercle de rayon l'unité, le segment sous-tendu par l'angle au centre. La corde est ainsi le double du sinus moderne de l'angle moitié.
Mais le sinus ne sera introduit que bien plus tard, au moyen âge.
Delambre propose d'ailleurs une singulière explication de l'origine de ce mot, bien différente de celle couramment admise. Le mot latin pour la corde inscrite est "inscripta". La moitié de la corde était donc désignée par "semis inscritpae" qui s'écrit en abrégé "s.ins." sigle devenu "sins" puis "sinus" pour être décliné!

Le théorème de Ptolémée relatif au quadrilatère convexe inscrit dans un cercle permettait de calculer facilement la valeur de la corde d'un angle somme de deux angles dont les cordes étaient connues.

le théorème de Ptolémée appliqué au calcul des cordes

Pour un cercle de rayon égal à l'unité, les cordes BC et CD de l'angle u en rouge et de l'angle v en bleu étant connues, les cordes AB et AD sont obtenues par le théorème de Pythagore et la corde BD de l'angle w en gris, somme des deux premiers, est donnée par (BCxAD+CDxAB)/2. 
Le théorème de Ptolémée permet d'établir les principales formules de trigonométrie. En effet il s'écrit en l’occurrence: 2sin(w/2) = (2sin(u/2)x2sin(180/2-v/2)+2sin(v/2)x2sin(180/2-u/2))/2 ce qui en notation moderne se simplifie en sin(u/2+v/2) = sin(u/2)cos(v/2)+sin(v/2)cos(u/2), formule bien connue des lycéens!
Ce qui est vrai pour la somme l'est aussi pour la différence.
Par bissection on pouvait donc rédiger des tables de cordes et on descendait ainsi jusqu'aux cordes de 1.5° et 0.75°. Pour la corde de 1° on faisait alors une interpolation entre ces deux valeurs.
La trisection de l'angle était reconnue impossible par la géométrie (au même titre que la duplication du cube ou la quadrature du cercle).

Ptolémée ne pouvait pas calculer la longueur SS' de sa figure en fonction de la déclinaison et de l'angle horaire mais ce n'était pas nécessaire pour sa construction. En notation moderne on a : L = sin(AH)cos(dec) où "AH" est l'angle horaire et "dec" la déclinaison du soleil.
La figure ci-dessous présente le dessin sur le plan méridien.

les segments en tireté bleu montrent les heures temporaires de jour et ceux en gris celles de nuit

Ici, pour une déclinaison égale à -17° et une latitude de 32°, l'heure temporaire de jour vaut 53 minutes 39 secondes et celle de nuit 67 minutes 21 secondes. La partie grise du rabattement de la course du soleil servira pour la déclinaison +17°.

Le magicien Ptolémée complète alors sa figure:

la construction de Ptolémée

Il projette le point S sur l'axe nord sud en P et sur l'axe vertical en Q. La demi-droite QS coupe le cercle de base en h et la demi-droite PS le coupe en v. Classiquement l'arc Zénith-h donne l'angle à l'astre (complément de la hauteur). Le point v détermine un arc sud-v qui donne par rapport au plan vertical l'équivalent d'un "angle à l'astre".
Puis sur la demi-droite PS, à partir de P il construit le point V' tel que PV'  = SS'. Soit a le point d'intersection de la droite CV' et du cercle de base: l'arc Zénith-a est le complément de l'azimut! 
Ensuite il construit sur la demi droite QS à partir de Q le point H' tel que QH' = SS'. Le point b, intersection de la droite CH' et du cercle de base, donne l'arc Sud-b, équivalent du complément de l'azimut pour un horizon qui serait le premier vertical et pour un un pôle qui serait le point sud!
Enfin, il détermine avec le compas le point O sur le cercle de base tel que SO = SS' et le point O' tel que l'angle SOC soit égal à l'angle OCO'. L'arc O-O' est l'angle à l'astre pour un horizon qui serait le plan méridien et pour un pôle qui serait le point est, le complément de l'azimut étant donné par l'arc Z-c.

On obtient ainsi sur le cercle de base les six grandeurs utiles à la construction du point d'ombre du sommet du gnomon sur les trois cadrans solaires.
La démonstration par Ptolémée de la pertinence de cette construction est quasiment impossible à suivre dans le texte: même Delambre y a perdu son latin et a eu recours à de longs calculs.

Cependant par une méthode géométrique moderne on peut mettre en évidence les angles recherchés et les justifier.

Tout d'abord on rappelle une égalité fondamentale de la trigonométrie sphérique: pour tout astre le produit du cosinus de la hauteur par le sinus de l'azimut est égal au produit du cosinus de la déclinaison par le sinus de l'angle horaire: cos(h)sin(A) = cos(dec)sin(H). Ces produits ne sont autres que la coordonnée de l'astre selon l'axe Ouest / Est. La figure ci-dessous, où on a dessiné à la fois les coordonnées horizontales et les coordonnées équatoriales, illustrent cette propriété.

 

cos(h)sin(A)=cos(dec)sin(H)

Ce préalable explicité, on procède à trois rabattements sur le plan méridien, d'abord autour de l'horizontale qui passe par la projection s de S, puis autour de la verticale passant par le même point et enfin autour de la droite qui joint le centre C au point s et qui est la trace du cercle hectémorion sur le plan méridien.
Il en découle la figure suivante.

les points S', H, V, O sont cocycliques

Pour l'angle horaire, en rouge:
le point V donne l'azimut (angle en bleu ciel) et donc son complément,
le point H donne la même grandeur mais par rapport au premier vertical (angle en rose),
et le point O donne la hauteur par rapport au plan méridien (angle en vert).

A partir de cette figure on retrouve celle du traité de Ptolémée en appliquant au point V une translation égale au vecteur QC pour obtenir V' et au point H une autre translation de vecteur PC pour obtenir le point H'.

la figure de Ptolémée justifiée

En prolongeant les demi-droites CV' et CH' on détermine alors sur le cercle de base les points a et b de Ptolémée. Le point O' s'obtient par l'angle alterne/interne à partir de O.
On peut aussi en appliquant le théorème de Thalès et les relations du triangle à la figure de Ptolémée démontrer sans difficulté que la position du point h répond bien à la formule de la hauteur
sin(hauteur) = sin(lat)sin(dec)+cos(lat)cos(dec)cos(H) où lat est la latitude, dec la déclinaison et H l'angle horaire.
Avec la même facilité on vérifie que la position du point a répond bien à la formule de l'azimut
tan(azimut) = sin(H)/(cos(H)sin(lat)-tan(dec)cos(lat)).
Les points v et b répondent aussi aux mêmes formules en remplaçant la latitude lat par lat + 90°.

L'intérêt de l'Analemme est bien la simplicité.

Dans une seconde partie Ptolémée propose une sorte d'instrument pratique pour déterminer rapidement les valeurs de ces arcs. Cet instrument ne prend en compte que les principaux climats et seulement les commencements des signes du zodiaque.
La figure ci-dessous explicite le processus à suivre.

l'instrument de Ptolémée pour la mesure des arcs cherchés

L'instrument présente les climats et les demi-cercles de la course du soleil pour les débuts des signes du zodiaque. Il reste à choisir les paramètres pour lesquels on veut tracer le point solaire sur le cadran, puis à partager en six parties l'arc parcouru par le soleil et enfin à faire la construction de Ptolémée.
L'arc de cercle gradué 45°/45° permet de mesurer les valeurs des arcs utiles.
Concurremment on peut avoir recours aux 49 (?) tables annexées!

table pour le commencement du cancer et le climat de 13h

La table ci-dessus est la reconstruction moderne de la seule table de Ptolémée qui nous soit parvenue.
L'écart avec les valeurs données par Ptolémée dépasse souvent le degré. Delambre s'est particulièrement étonné de l'imprécision du nombre retenu par Ptolémée pour la deuxième heure du cadran vertical: 69°50' au lieu, d'après lui 79°10'. Il attribue l'erreur au copiste. En réalité la bonne réponse semble bien être 74°40'...

Ptolémée n'explicite pas le détail du tracé des cadrans solaires qui devait déjà être bien connu.

La figure ci-dessous présente le tracé pour le cadran horizontal: 

la construction du point d'ombre sur le cadran horizontal

 L'arc Z-a en bleu donne, depuis l'est, la position du point A. De ce point une rotation de 90° autour de l'axe vertical OZ donne le point A'. De ce point on trace la demi-droite faisant avec OA' un angle égal à l'arc Z-h en gris. Le point d'ombre est à l'intersection de cette demi-droite avec la droite OA.

le cadran solaire horizontal d'heures temporaires

La figure ci-dessous présente le tracé pour le cadran vertical:

la construction du point d'ombre sur le cadran vertical

 L'arc Sud-b en rouge donne, depuis l'est, la position du point B. De ce point une rotation de 90° autour de l'axe horizontal nord sud donne le point B'. de ce point on trace la demi-droite faisant avec OB' un angle égal à l'arc Sud-v en gris. Le point d'ombre est à l'intersection de cette demi-droite avec la droite OB.

le cadran solaire vertical d'heures temporaires

La figure ci-dessous présente le tracé pour le cadran oriental:

la construction du point d'ombre sur le cadran oriental

Par une rotation d'angle égal à l'arc o-o' autour de l'axe passant par le point est et perpendiculaire au plan de l'hectémorion, on construit le point d'ombre à l'intersection de la droite Os.

le cadran solaire oriental d'heures temporaires

Il se trouve que le point d'ombre, lorsque l'on modifie la déclinaison du soleil, décrit pour la même heure temporaire une courbe qui est très proche d'un segment de droite. C'est là une sorte de "miracle trigonométrique" qui confère une légitimation aux heures temporaires.

les lignes horaires pour les heures temporaires

Pour que la courbe décrite par le point d'ombre, en rouge, soit une droite il faut et il suffit que l'arc décrit par le soleil lorsque la déclinaison varie, pour la même heure temporaire, soit un grand cercle de la sphère. Or si on construit pour la même heure temporaire trois positions du soleil pour trois déclinaisons différentes, ici S, S1 et S2, on détermine le cercle en gris dont le centre C' ne coïncide pas avec le centre C de la sphère: la ligne horaire n'est pas une droite!
Mais si on choisit deux valeurs opposées de la déclinaison pour deux points, ici S et S', et la valeur nulle pour le troisième point (c'est à dire le soleil à l'équinoxe), alors ces trois points déterminent un grand cercle. Il en découle que pour deux valeurs opposées de la déclinaison, les deux points d'ombre sur le cadran et le point équinoxial sont alignés. Ce segment connait une légère rotation autour du point équinoxial quand l'heure temporaire change.
La partie droite de la figure présente en rouge, après dilatation pour la lisibilité, les lignes horaires pour un cadran sphérique à la latitude de 49° centré sur le sommet du gnomon. Ces lignes ont un aspect sinusoïdal qui reste à préciser.
Un cadran qui serait dessiné avec des segments de droite ne serait rigoureusement juste que pour les équinoxes et les solstices. L'écart est le plus grand pour la troisième heure temporaire et pour les déclinaisons voisines de +/- 15° (début février et mi-août).
Au printemps et en été ce cadran est très légèrement en retard le matin sur le soleil et en avance l'après-midi. C'est l'inverse en automne et en hiver. 
L'écart est d'autant plus important que la latitude est plus élevée: pour le climat de 16h, le plus septentrional du traité (49°), il reste inférieur, d'après Delambre, à la minute équinoxiale mais pour les climats du monde méditerranéen il est indécelable.

la Tour des Vents et ses cadrans d'heures temporaires à Athènes

Les cadrans solaires de la Tour des Vents sont-ils les seuls vestiges de cadrans construits conformément au Traité de L'Analemme de Ptolémée?

Deuxièmes éclipses de soleil et de lune en 2015

Le 13 septembre 2015 a lieu une éclipse de soleil.

Mais la lune est loin de la terre, à 405.500 km, presque à son apogée, et son disque n'est pas assez grand pour recouvrir complètement celui du soleil.
L'éclipse n'est donc pas totale.

Le soleil est entré le 7 septembre dans la partie de l'écliptique voisine du nœud ascendant de l'orbite lunaire. Traverser cette zone lui demande 35 jours et il ne peux la franchir sans être éclipsé par la lune lors de la nouvelle lune qui a lieu le 13 septembre à 6h41 UTC.

Soleil et lune sont alors assez éloignés du nœud: 11.2° (le soleil ne l'atteint que le 24/09 à 4h47).
La latitude de la lune est donc importante en valeur absolue, presque un degré, et l'axe du cône d'ombre de la lune passe à coté de la terre: l'éclipse n'est annulaire en aucun point de la terre.
L'éclipse n'est que partielle.

La nouvelle lune se produisant avant le passage au nœud ascendant la latitude est négative et l'éclipse concerne donc l’hémisphère sud.

L'éclipse commence 2.000 km au nord de la ville du Cap à 4h41 UTC, atteint les pays du sud de l'Afrique et Madagascar puis l'Antarctique oú elle se termine à 9h06.

L'éclipse est maximum à 6h54 UTC, elle quitte Le Cap alors que le soleil est au zénith de Colombo

Une demi lunaison plus tard, la lune s'approche de l'autre nœud de son orbite, mais le cône d'ombre de la terre se trouve dans la partie de l'écliptique voisine de ce nœud puisque le soleil n'a pas fini de traverser la zone voisine du nœud ascendant (il ne s'en échappera que le 12 octobre, juste avant la nouvelle lune du 13).
A son tour, la lune est éclipsée lors de la pleine lune qui se produit le 28 septembre à 2h51 UTC (4h51, heure légale en Europe). Elle est alors très proche du périgée, à 357.000 km de la terre, et son diamètre apparent est donc particulièrement important.
Ceci se passe après le nœud descendant, à 4.1° de celui-ci. Ombre et lune sont ainsi assez proches du nœud et la latitude de la lune est faible: -0.3°.
L'éclipse de lune est alors totale.

Sion (CH), 28/09/2015, 3h07m (heure légale). La lune, éclipsée par la pénombre, entame sa traversée de l'ombre de la Terre.

 La ligne rouge est l'écliptique, les lignes noires représentent le parcours de la lune. L'éclipse est maximale à 4h47.

Sion (CH) trajectoire de la lune dans le ciel pendant l'éclipse du 28/09/2015 de 3h07 à 6h27 (heures légales)

L'écliptique, en rouge, et l'orbite de la lune, en gris, sont dessinés pour le moment du maximum à 4h47. Le disque de l'ombre de la terre, de couleur rouge, n'est bien sûr réellement visible que dans sa partie qui éclipse la lune.

La prochaine éclipse totale de lune visible en Europe aura lieu le 27 juillet 2018. A Sion (CH) La lune se lèvera, déjà éclipsée, à 21h. Ce sera une éclipse exceptionnellement forte, le centre de la lune passant très près du centre de l'ombre!

les astrolabes universels

L'astrolabe traditionnel, qui remonte à l'Antiquité, donne une représentation de la position des astres établie en un lieu donné qui n'est valable que pour la latitude de ce lieu. Cet outil astronomique comprend deux parties principales. Si celle dénommée "araignée", qui est la carte des étoiles, est universelle, l'autre appelée "tympan" présente le réseau des méridiens et parallèles du lieu, dont le dessin dépend de la hauteur du pôle céleste au dessus de l'horizon.
Les astrolabistes construisaient donc plusieurs tympans à utiliser selon la latitude du lieu d' observation.

astrolabe d'Abu-Bakr (1216), musée Paul Dupuy Toulouse

l'araignée et ses 28 étoiles redessinée par R. D'Hollander

La position de l'étoile est déterminée par l'extrémité du crochet qui la porte. L'étoile n°5 est Sirius. La n°12, Antarès, est celle dont la déclinaison négative est la plus importante (-24°), pratiquement égale à celle du tropique du Capricorne. Les astrolabes ne représentent pas les étoiles de déclinaison encore plus négative en raison de la déformation excessive due à la projection stéréographique.
Le cercle intérieur décalé est l'écliptique.

Au début du deuxième millénaire des astronomes vivant à Tolède, Ali ibn Khalaf et Az-Zarqalla (Arzaquiel 1029-1087), imaginent une autre projection qui, elle, permet de s'affranchir des contraintes de la latitude. L'instrument fonctionnera à toutes les latitudes: il sera "universel".

On appelle colure des solstices le cercle céleste méridien qui passe par les points solsticiaux, là ou se trouve le soleil le 21 juin et le 21 décembre. La direction du point gamma est constamment perpendiculaire au plan de ce colure. Les nouveaux astrolabistes projettent alors sur ce plan du colure, depuis le point gamma, les étoiles situées au delà du plan et, depuis le point symétrique, les autres. Les étoiles sont enchevêtrées, ce qui n'est pas un grand inconvénient, mais celles de l'hémisphère céleste sud peuvent aussi être dessinées.
Une fois cette projection réalisée on fait coïncider le plan du colure avec le plan du méridien du lieu, c'est à dire la direction du point gamma avec la direction est-ouest. On a le choix entre l'est ou l'ouest pour le point gamma. La littérature mentionne que les inventeurs de la projection ont choisi l'ouest. Ici on a retenu l'est. La latitude intervient pour tracer l'horizon du lieu sur l'image de la sphère céleste.
Il reste à mettre en marche l'horloge sidérale, le temps sidéral local (tsl) de départ étant ici 18h.
D'une projection sur le plan du colure on va passer à une projection sur le plan du méridien du lieu.

la projection depuis le point gamma sur le plan du colure (à g.) et la projection traditionnelle (à d.)

A gauche, la projection se fait en deux temps.
D'abord une projection depuis le point gamma, sur le plan du colure des solstices, dessiné en gris, (le temps sidéral local vaut alors 18h), l'image de l'étoile, en bleue, est figurée en E0.
Puis, pour la valeur, ici, de 21h du temps sidéral local, une projection depuis l'est, sur le plan du méridien, l'image de l'étoile est alors dessinée en E1.
 L'horizon est le cercle vert, sa projection est un segment de droite.
La ligne de déclinaison égale, notée dec, se projette suivant l'arc de cercle en vert clair. Le centre noté C de ce cercle est à la distance 1/sin(dec) du centre de la sphère et son rayon est égal à 1/tan(dec). Il coupe l'axe polaire en H à la cote (1-cos(dec))/sin(dec) soit tan(dec/2). Il en va de même pour la ligne de hauteur égale (almicantarat) qui se projette suivant l'arc de cercle en vert foncé et dont les caractéristiques sont analogues en remplaçant la déclinaison par la hauteur. Ces arcs de cercle sont indépendants de la latitude et ils sont interchangeables par une rotation d'angle égal au complément de la latitude.

A droite la projection de l'étoile se fait depuis le pôle céleste sud sur le plan de l'équateur en E0 et E1. Les almicantarats sont des cercles, centrés sur la ligne nord sud à une distance du centre de l'astrolabe qui est directement fonction de la latitude, et dont les rayons le sont aussi. L'horizon, par exemple, a son centre à la distance 1/tan(lat) et son rayon est égal à 1/sin(lat), où "lat" est la latitude.

L'astrolabe universel ainsi imaginé par Arzaquiel est appelé saphaea. 500 ans plus tard il reçoit dans le monde latin le nom d'"astrolabe catholique" (catholique pour universel).

saphaea, arcs horaires en rouge et arcs de déclinaison en vert. 10h50, Sirius se lève

La saphaea est équipée de la regula qui peut tourner autour du centre. Celle-ci porte soit un curseur mobile perpendiculaire, soit, en son milieu, une potence équipée du brachiolus, bras articulé qui permet de pointer la position d'un astre.
En noir le point S est la position, dans le plan du colure, du soleil sur l'écliptique , fonction de sa déclinaison au jour de l'observation. Dans le plan du méridien le soleil, en rouge, se déplace au cours de la journée sur l'arc de cercle correspondant à cette déclinaison, en rouge pour le jour et en gris pour la nuit. Les heures de lever et coucher sont lues sur la regula après l'avoir placée sur l'horizon.
La projection induit une graduation qui obéit à la loi de tan(A/2).
Pour une heure donnée, la hauteur et l'azimut sont mis en évidence en imprimant une rotation à la régula pour l'amener sur l'équateur céleste, le point solaire étant entraîné dans le mouvement. On utilise alors les arcs horaires et de déclinaison comme s'ils étaient les arcs d'azimut et de hauteur.
La figure présente les mêmes éléments pour l'étoile Sirius.

après rotation de la regula, la pointe du brachiolus donne hauteur et azimut

Si au lieu de l'heure on connait la hauteur ou l'azimut il faut procéder par méthode itérative pour placer le point solaire et déterminer l'heure.
La saphaea est particulièrement précise pour les heures proches de midi ou de minuit. Par contre le resserrement exagéré des arcs horaires aux environs de 6h et 18h est un inconvénient.

A la Renaissance la géométrie a fait de notables progrès et on sait tracer des ellipses. Cette circonstance conduit l'astronome espagnol Juan de Rojas à délaisser la projection stéréographique pour retenir une projection orthographique depuis un point situé à l'infini dans la direction du point gamma. Les courbes de déclinaison constante deviennent des segments de droite et les arcs horaires des ellipses.
Cette projection avait déjà été utilisée par les Anciens et Ptolémée y avait consacré un ouvrage que malheureusement les traductions successives de langue en langue rendent un peu abscons.

la projection orthographique de l'astrolabe de Rojas

Sur certains astrolabes construits sur ces bases les ellipses sont remplacées par des arcs de cercle plus faciles à dessiner, ce qui induit des écarts appréciables pour les seules hautes latitudes. Pour 8h p.m. on a dessiné en rouge l'arc de cercle et en bleu la courbe classique proche de l'ellipse composée de quatre cercles tangents entre eux.

l'astrolabe de Rojas stylisé

Le brachiolus est inutile. La hauteur mesurée sur le curseur donne l'heure et inversement.
Pour l'azimut on a recours au stratagème utilisé pour la saphaea en imprimant une rotation à la regula après avoir judicieusement calé le curseur et repéré le point solaire.
La projection induit une graduation qui obéit à la loi de sin(A).

l'azimut indiqué par l'arc horaire désigné par le point solaire après rotation

A l'inverse de la saphaea, dans cette projection le resserrement des arcs concerne les heures proches de midi et minuit, la précision étant la meilleure vers 6h ou 18h.

Il faut attendre l'année 1701 et le mathématicien et physicien extrêmement fécond Philippe de La Hire (1640-1718) pour que soit retenue une projection qui conduit à un écartement presque constant des arc horaires. La Hire prend comme "œil" de la projection le point tel que l'arc horaire de 9h, qui correspond au huitième de la journée, coupe l'équateur céleste au milieu entre le centre et le bord de l'astrolabe. Tous calculs faits cet "œil" se trouve à une distance exprimée en rayon de la sphère, égale à 1+rac(2)/2 = 1.707 du centre de la sphère céleste. Les arcs de déclinaison et les arcs horaires sont des arcs d'ellipses excentrées.

les trois projections des astrolabes universels

La projection de La Hire est un bon compromis. Cependant l'espacement des arcs horaires n'est qu'approximativement constant. La figure ci dessous montre qu'en plaçant l’œil à 1.677 du centre au lieu de 1.707 on a un meilleur résultat mais la formulation mathématique est transcendante. De multiples autres "yeux" ont par la suite été retenus pour cartographier la terre depuis l'espace.

optimisation de la position de l’"œil"

l'astrolabe de La Hire fonctionne comme la saphaea

La projection induit une graduation qui obéit à la loi k.sin(A)/(k+cos(A)) où k est la distance de l’œil au centre, exprimée en rayon de la sphère, égale à 1+rac(2)/2. Pour k infini (Rojas) on retrouve la loi sin(A) et pour k=1 (Arzaquiel), la loi sin(A)/(1+cos(A)) soit tan(A/2).
A l'époque de La Hire l'astrolabe n'est plus en vogue mais la projection qu'il a mise au point est encore largement utilisée pour représenter une sphère complète ou partielle.

le planisphère céleste en coordonnées écliptiques de La Hire, 1705

Ces astrolabes universels sont des abaques destinés à des calculs et ne servent pas à viser les astres. Ils présentent un aspect très simple et l'opération de rotation permet de faire jouer à un seul réseau d'arcs deux rôles: le premier comme repère pour les coordonnées équatoriales, ascension droite, déclinaison et angle horaire, et le second pour les coordonnées locales, hauteur et azimut. Mais ils sont de ce fait un peu plus compliqués à utiliser que l'astrolabe classique.

Une solution consiste alors à individualiser les deux réseaux de coordonnées en dessinant le réseau des coordonnées équatoriales sur un disque mobile réglé sur la latitude du lieu, ce disque constituant alors une araignée semblable à celle de l'astrolabe classique. Le suspensoir est solidaire du disque portant le réseau des coordonnées locales. L'astrolabe est tenu verticalement et la regula est transformée en alidade à pinnules: l'objet est complet.

Un tel astrolabe, dans la version saphaea, a été construit à Alep en 1328 par l'astronome Ibn al Sarray. Cet objet, mentionné par D'Hollander dans son ouvrage de référence "L'Astrolabe" est conservé au musée Benaki d'Athènes.

 

astrolabe universel direct à projection stéréographique type saphaea

il manque à cet exemplaire du musée d'Istanbul son alidade

De la même façon on peut utiliser un disque mobile pour la version de Rojas.

astrolabe universel direct à projection orthographique type Rojas

Ce dernier type d'astrolabe a beaucoup de points communs avec les "analemmes" étudiés par Ptolémée.

L'astrolabe, même pas mort!

En effet deux "astrolabistes" modernes, chercheurs au Laboratoire CERMA de l’École Nationale Supérieure d'Architecture de Nantes, ont conçu en 1979 un abaque donnant, pour toute latitude et à tout instant, l'azimut et la hauteur du soleil. L'appareil permet de visualiser et de calculer les ombres portées par les bâtiments.
Ce "Girasol" n'est rien moins qu'une saphaea limitée à l'astre du jour.

le Girasol, 1979... 900 ans après Arzaquiel