Le Traité de l'Analemme, par Ptolémée

Claude Ptolémée (90-168) vivait à Alexandrie. Son nom dérive du lieu de sa naissance, Ptolémaïs près de Thèbes en Haute Égypte.
Il était de citoyenneté romaine car depuis les suicides de Marc-Antoine et Cléopâtre consécutifs au désastre de leur armée à Actium, en -31, face à Octave (le futur empereur Auguste), l’Égypte est romaine.
Mais ses origines sont gréco-égyptiennes puisque Cléopâtre était la dernière représentante de la dynastie des Ptolémée qui remontait au partage de l'empire d'Alexandre Le Grand, proclamé pharaon en -331.

Ses écrits astronomiques, dont le Traité de l'Analemme, sont rédigés en grec.
L'Analemme, ici, n'a aucun lien autre que l'homonymie avec la célèbre courbe en huit.
 
La librairie Blanchard à Paris diffuse un ouvrage édité en 2009 par les Editions Bergeret à Mérignac intitulé "Claude Ptolémée Livre de L'Analemme". Il s'agit d'une traduction du latin en français par Jean Peyroux (1925-2012), ingénieur des Arts et Métiers, d'un texte publié en 1562 à Rome par Frédéric Commandin, mathématicien italien. Cet ouvrage est remarquable et on cite ici le début de l' "avertissement du traducteur":

" Le texte grec de Claude Ptolémée ne nous est pas parvenu. Au XVI ème siècle, l'italien Frédéric Commandin, ayant découvert un manuscrit latin ayant pour titre Analemme de Claude Ptolémée, décida de le publier. Ce manuscrit latin est une mauvaise traduction, d'ailleurs incomplète, de manuscrits arabes du texte grec qui ont disparu. Le traité latin, avec des figures obscures et compliquées, fut complété et commenté par Commandin souvent peu clair lui aussi."

Dès 1817 Delambre (1749-1822), astronome et mathématicien français, avait analysé sans concession le livre de Commandin dans son Histoire de l'Astronomie Ancienne. Ces deux ouvrages permettent de reconstituer la science gnomonique des Grecs (et de faire litière des approximations émises sur l'Analemme de Ptolémée).

Il apparait que l'Analemme n'est autre qu'un traité justifiant et explicitant la marche à suivre pour la construction géométrique, sur un cadran solaire disposé dans un plan horizontal ou vertical plein sud ou vertical plein est, du point d'ombre portée par le sommet du gnomon (tige perpendiculaire au plan du cadran).
Le traité se terminait par des tables numériques donnant les valeurs à retenir pour les principaux "climats", pour le début de chaque signe du zodiaque et pour chaque heure. Ces tables permettaient ainsi de tracer rapidement des cadrans solaires dont la précision quoique relative était suffisante. Elles ont toutes disparu sauf celle correspondant au commencement du signe du Cancer pour le climat de 13h.

Il faut préciser que le cadran solaire à style polaire parallèle à l'axe du monde n'existait pas encore du temps des Grecs et que les heures courantes étaient des heures dites temporaires car égales à la douzième partie de la durée variable entre lever et coucher du soleil. Quant à la notion de "climat", il s'agit d'une façon de chiffrer la latitude par la durée en un lieu, en heures équinoxiales (égales), du temps séparant lever et coucher du soleil le jour du solstice d'été. Ainsi le climat de 13h correspond à la latitude de 16.5° pour une obliquité chiffrée à 23.83° par Ptolémée.

Ptolémée repère la position du soleil à un instant donné par 3 grands cercles qui, pour deux d'entre eux, ne sont pas ceux utilisés de nos jours, mais qui se révèlent très judicieux pour les cadrans solaires. Ces 3 cercles sont le "cercle de descente" qui passe par le zénith et le nadir (pour nous le vertical de l'astre), le "cercle horaire" qui passe par les points nord et sud (rien à voir avec le nôtre) et le "cercle hectémorion" qui passe par les points est et ouest.

les trois grands cercles de Ptolémée et les trois arcs à mesurer

Ptolémée a mis au point une méthode employant règle et compas pour représenter la valeur des arcs de grand cercle séparant l'astre du zénith en bleu (notre angle à l'astre), du point sud en rouge et du point est en vert. Il emploie une projection orthographique selon la direction est ouest sur le plan du méridien et procède à un rabattement sur ce plan du chemin suivi par le soleil pendant la journée.

en jaune la course du soleil depuis son lever jusqu'à midi, en rouge son rabattement sur le plan méridien

L'arc en bleu est le cercle horaire au sens moderne. Le soleil "S" se projette en "s" et se rabat en "S' ". La longueur du segment sS', égale par construction à celle du segment sS joue un rôle essentiel dans la suite.
La mathématique des Anciens Grecs ne connaissait pas les chiffres d'aujourd'hui: on utilisait les lettres de l'alphabet. Leur trigonométrie ne connaissait pas les lignes trigonométriques modernes: on utilisait la seule notion de "corde" qui est, dans un cercle de rayon l'unité, le segment sous-tendu par l'angle au centre. La corde est ainsi le double du sinus moderne de l'angle moitié.
Mais le sinus ne sera introduit que bien plus tard, au moyen âge.
Delambre propose d'ailleurs une singulière explication de l'origine de ce mot, bien différente de celle couramment admise. Le mot latin pour la corde inscrite est "inscripta". La moitié de la corde était donc désignée par "semis inscritpae" qui s'écrit en abrégé "s.ins." sigle devenu "sins" puis "sinus" pour être décliné!

Le théorème de Ptolémée relatif au quadrilatère convexe inscrit dans un cercle permettait de calculer facilement la valeur de la corde d'un angle somme de deux angles dont les cordes étaient connues.

le théorème de Ptolémée appliqué au calcul des cordes

Pour un cercle de rayon égal à l'unité, les cordes BC et CD de l'angle u en rouge et de l'angle v en bleu étant connues, les cordes AB et AD sont obtenues par le théorème de Pythagore et la corde BD de l'angle w en gris, somme des deux premiers, est donnée par (BCxAD+CDxAB)/2. 
Le théorème de Ptolémée permet d'établir les principales formules de trigonométrie. En effet il s'écrit en l’occurrence: 2sin(w/2) = (2sin(u/2)x2sin(180/2-v/2)+2sin(v/2)x2sin(180/2-u/2))/2 ce qui en notation moderne se simplifie en sin(u/2+v/2) = sin(u/2)cos(v/2)+sin(v/2)cos(u/2), formule bien connue des lycéens!
Ce qui est vrai pour la somme l'est aussi pour la différence.
Par bissection on pouvait donc rédiger des tables de cordes et on descendait ainsi jusqu'aux cordes de 1.5° et 0.75°. Pour la corde de 1° on faisait alors une interpolation entre ces deux valeurs.
La trisection de l'angle était reconnue impossible par la géométrie (au même titre que la duplication du cube ou la quadrature du cercle).

Ptolémée ne pouvait pas calculer la longueur SS' de sa figure en fonction de la déclinaison et de l'angle horaire mais ce n'était pas nécessaire pour sa construction. En notation moderne on a : L = sin(AH)cos(dec) où "AH" est l'angle horaire et "dec" la déclinaison du soleil.
La figure ci-dessous présente le dessin sur le plan méridien.

les segments en tireté bleu montrent les heures temporaires de jour et ceux en gris celles de nuit

Ici, pour une déclinaison égale à -17° et une latitude de 32°, l'heure temporaire de jour vaut 53 minutes 39 secondes et celle de nuit 67 minutes 21 secondes. La partie grise du rabattement de la course du soleil servira pour la déclinaison +17°.

Le magicien Ptolémée complète alors sa figure:

la construction de Ptolémée

Il projette le point S sur l'axe nord sud en P et sur l'axe vertical en Q. La demi-droite QS coupe le cercle de base en h et la demi-droite PS le coupe en v. Classiquement l'arc Zénith-h donne l'angle à l'astre (complément de la hauteur). Le point v détermine un arc sud-v qui donne par rapport au plan vertical l'équivalent d'un "angle à l'astre".
Puis sur la demi-droite PS, à partir de P il construit le point V' tel que PV'  = SS'. Soit a le point d'intersection de la droite CV' et du cercle de base: l'arc Zénith-a est le complément de l'azimut! 
Ensuite il construit sur la demi droite QS à partir de Q le point H' tel que QH' = SS'. Le point b, intersection de la droite CH' et du cercle de base, donne l'arc Sud-b, équivalent du complément de l'azimut pour un horizon qui serait le premier vertical et pour un un pôle qui serait le point sud!
Enfin, il détermine avec le compas le point O sur le cercle de base tel que SO = SS' et le point O' tel que l'angle SOC soit égal à l'angle OCO'. L'arc O-O' est l'angle à l'astre pour un horizon qui serait le plan méridien et pour un pôle qui serait le point est, le complément de l'azimut étant donné par l'arc Z-c.

On obtient ainsi sur le cercle de base les six grandeurs utiles à la construction du point d'ombre du sommet du gnomon sur les trois cadrans solaires.
La démonstration par Ptolémée de la pertinence de cette construction est quasiment impossible à suivre dans le texte: même Delambre y a perdu son latin et a eu recours à de longs calculs.

Cependant par une méthode géométrique moderne on peut mettre en évidence les angles recherchés et les justifier.

Tout d'abord on rappelle une égalité fondamentale de la trigonométrie sphérique: pour tout astre le produit du cosinus de la hauteur par le sinus de l'azimut est égal au produit du cosinus de la déclinaison par le sinus de l'angle horaire: cos(h)sin(A) = cos(dec)sin(H). Ces produits ne sont autres que la coordonnée de l'astre selon l'axe Ouest / Est. La figure ci-dessous, où on a dessiné à la fois les coordonnées horizontales et les coordonnées équatoriales, illustrent cette propriété.

 

cos(h)sin(A)=cos(dec)sin(H)

Ce préalable explicité, on procède à trois rabattements sur le plan méridien, d'abord autour de l'horizontale qui passe par la projection s de S, puis autour de la verticale passant par le même point et enfin autour de la droite qui joint le centre C au point s et qui est la trace du cercle hectémorion sur le plan méridien.
Il en découle la figure suivante.

les points S', H, V, O sont cocycliques

Pour l'angle horaire, en rouge:
le point V donne l'azimut (angle en bleu ciel) et donc son complément,
le point H donne la même grandeur mais par rapport au premier vertical (angle en rose),
et le point O donne la hauteur par rapport au plan méridien (angle en vert).

A partir de cette figure on retrouve celle du traité de Ptolémée en appliquant au point V une translation égale au vecteur QC pour obtenir V' et au point H une autre translation de vecteur PC pour obtenir le point H'.

la figure de Ptolémée justifiée

En prolongeant les demi-droites CV' et CH' on détermine alors sur le cercle de base les points a et b de Ptolémée. Le point O' s'obtient par l'angle alterne/interne à partir de O.
On peut aussi en appliquant le théorème de Thalès et les relations du triangle à la figure de Ptolémée démontrer sans difficulté que la position du point h répond bien à la formule de la hauteur
sin(hauteur) = sin(lat)sin(dec)+cos(lat)cos(dec)cos(H) où lat est la latitude, dec la déclinaison et H l'angle horaire.
Avec la même facilité on vérifie que la position du point a répond bien à la formule de l'azimut
tan(azimut) = sin(H)/(cos(H)sin(lat)-tan(dec)cos(lat)).
Les points v et b répondent aussi aux mêmes formules en remplaçant la latitude lat par lat + 90°.

L'intérêt de l'Analemme est bien la simplicité.

Dans une seconde partie Ptolémée propose une sorte d'instrument pratique pour déterminer rapidement les valeurs de ces arcs. Cet instrument ne prend en compte que les principaux climats et seulement les commencements des signes du zodiaque.
La figure ci-dessous explicite le processus à suivre.

l'instrument de Ptolémée pour la mesure des arcs cherchés

L'instrument présente les climats et les demi-cercles de la course du soleil pour les débuts des signes du zodiaque. Il reste à choisir les paramètres pour lesquels on veut tracer le point solaire sur le cadran, puis à partager en six parties l'arc parcouru par le soleil et enfin à faire la construction de Ptolémée.
L'arc de cercle gradué 45°/45° permet de mesurer les valeurs des arcs utiles.
Concurremment on peut avoir recours aux 49 (?) tables annexées!

table pour le commencement du cancer et le climat de 13h

La table ci-dessus est la reconstruction moderne de la seule table de Ptolémée qui nous soit parvenue.
L'écart avec les valeurs données par Ptolémée dépasse souvent le degré. Delambre s'est particulièrement étonné de l'imprécision du nombre retenu par Ptolémée pour la deuxième heure du cadran vertical: 69°50' au lieu, d'après lui 79°10'. Il attribue l'erreur au copiste. En réalité la bonne réponse semble bien être 74°40'...

Ptolémée n'explicite pas le détail du tracé des cadrans solaires qui devait déjà être bien connu.

La figure ci-dessous présente le tracé pour le cadran horizontal: 

la construction du point d'ombre sur le cadran horizontal

 L'arc Z-a en bleu donne, depuis l'est, la position du point A. De ce point une rotation de 90° autour de l'axe vertical OZ donne le point A'. De ce point on trace la demi-droite faisant avec OA' un angle égal à l'arc Z-h en gris. Le point d'ombre est à l'intersection de cette demi-droite avec la droite OA.

le cadran solaire horizontal d'heures temporaires

La figure ci-dessous présente le tracé pour le cadran vertical:

la construction du point d'ombre sur le cadran vertical

 L'arc Sud-b en rouge donne, depuis l'est, la position du point B. De ce point une rotation de 90° autour de l'axe horizontal nord sud donne le point B'. de ce point on trace la demi-droite faisant avec OB' un angle égal à l'arc Sud-v en gris. Le point d'ombre est à l'intersection de cette demi-droite avec la droite OB.

le cadran solaire vertical d'heures temporaires

La figure ci-dessous présente le tracé pour le cadran oriental:

la construction du point d'ombre sur le cadran oriental

Par une rotation d'angle égal à l'arc o-o' autour de l'axe passant par le point est et perpendiculaire au plan de l'hectémorion, on construit le point d'ombre à l'intersection de la droite Os.

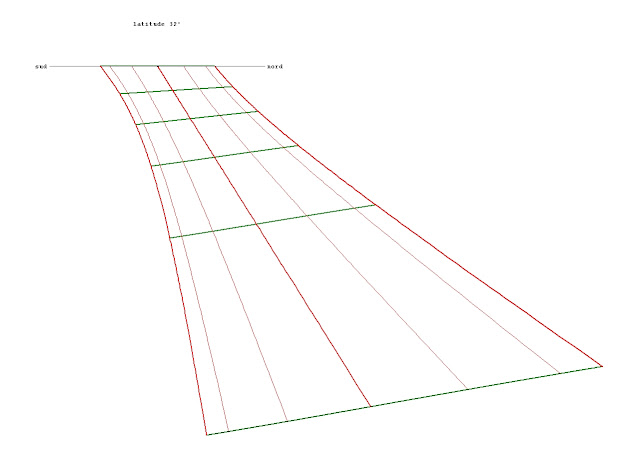le cadran solaire oriental d'heures temporaires

Il se trouve que le point d'ombre, lorsque l'on modifie la déclinaison du soleil, décrit pour la même heure temporaire une courbe qui est très proche d'un segment de droite. C'est là une sorte de "miracle trigonométrique" qui confère une légitimation aux heures temporaires.

les lignes horaires pour les heures temporaires

Pour que la courbe décrite par le point d'ombre, en rouge, soit une droite il faut et il suffit que l'arc décrit par le soleil lorsque la déclinaison varie, pour la même heure temporaire, soit un grand cercle de la sphère. Or si on construit pour la même heure temporaire trois positions du soleil pour trois déclinaisons différentes, ici S, S1 et S2, on détermine le cercle en gris dont le centre C' ne coïncide pas avec le centre C de la sphère: la ligne horaire n'est pas une droite!
Mais si on choisit deux valeurs opposées de la déclinaison pour deux points, ici S et S', et la valeur nulle pour le troisième point (c'est à dire le soleil à l'équinoxe), alors ces trois points déterminent un grand cercle. Il en découle que pour deux valeurs opposées de la déclinaison, les deux points d'ombre sur le cadran et le point équinoxial sont alignés. Ce segment connait une légère rotation autour du point équinoxial quand l'heure temporaire change.
La partie droite de la figure présente en rouge, après dilatation pour la lisibilité, les lignes horaires pour un cadran sphérique à la latitude de 49° centré sur le sommet du gnomon. Ces lignes ont un aspect sinusoïdal qui reste à préciser.
Un cadran qui serait dessiné avec des segments de droite ne serait rigoureusement juste que pour les équinoxes et les solstices. L'écart est le plus grand pour la troisième heure temporaire et pour les déclinaisons voisines de +/- 15° (début février et mi-août).
Au printemps et en été ce cadran est très légèrement en retard le matin sur le soleil et en avance l'après-midi. C'est l'inverse en automne et en hiver. 
L'écart est d'autant plus important que la latitude est plus élevée: pour le climat de 16h, le plus septentrional du traité (49°), il reste inférieur, d'après Delambre, à la minute équinoxiale mais pour les climats du monde méditerranéen il est indécelable.

la Tour des Vents et ses cadrans d'heures temporaires à Athènes

Les cadrans solaires de la Tour des Vents sont-ils les seuls vestiges de cadrans construits conformément au Traité de L'Analemme de Ptolémée?