le cadran solaire azimutal à gnomon fixe

florilège de cubiques circulaires focales partageant foyer et asymptote

Il s'agit dans cet article de la mise en œuvre d'une quatrième coïncidence trigonométrique!

Un premier "miracle" a permis de construire le quadrant universel, basé sur la hauteur du soleil, dont les lignes des heures inégales sont faciles à tracer car il s'agit à très peu de choses près d'arcs de cercle (voir à ce sujet l'article du présent blog en date du 17-10-2014 intitulé "La magie du quadrant d'heures inégales"). Cet objet individuel, sorte de montre de l'Antiquité et du Moyen Age, devait être assez répandu ainsi que ses variantes: quadrant d'heures égales, quadrant du tableau des ambassadeurs...etc (voir à ce sujet l'article du présent blog en date du 19/11/2014 intitulé "les cadrans de hauteur à style").

Un second "miracle" a conféré une grande simplicité d’exécution aux cadrans de l'Antiquité, à gnomon perpendiculaire, car les lignes des heures inégales sont alors à très peu de choses près des segments de droite. Il s'agit là de cadrans fixes, car il faut les orienter exactement, et souvent monumentaux. Tel le cadran horizontal d'Auguste au Champ de Mars à Rome ou ceux, verticaux, de la Tour des Vents à Athènes. Pour ces cadrans c'est l’extrémité du gnomon qui désigne l'heure sur un abaque tracé sur la table.
Le traité de Ptolémée, "L'Analemme", donne la méthode utile au dessin de ces abaques (voir à ce sujet l'article du présent blog en date du 12-11-2015 intitulé "Le Traité de l'Analemme, par Ptolémée").

Bien plus tardivement on imaginera de remplacer le gnomon perpendiculaire par un style pointé vers le pôle nord et donc incliné sur la table du cadran. On constatera alors que les lignes des heures classiques sont les droites que forme l'ombre de l'axe du monde matérialisé par le style. Mais il ne s'agira plus alors de "miracle" parce que cela résulte de la simple trigonométrie.

Un troisième "miracle" a encore présidé à la mise au point de l'anneau de paysan et de ses dérivés tels la bague solaire... 

La coïncidence qui nous occupe ici concerne un cadran d'heures classiques basé non plus sur la hauteur du soleil mais sur son autre coordonnée locale: son azimut.
A la différence des autres cadrans d'azimut (cadran analemmatique, cadran d'Oughtred, cadran orthographique) qui résultent d'une projection, l'abaque de celui-ci est fait de cercles concentriques autour du pied du gnomon.
L'azimut A est donné par la formule tanA = sinH / (cosH.sinl - tand.cosl) où H est l'angle horaire, l la latitude et d la déclinaison.
Traçons un cercle de référence, de rayon quelconque, centré sur le pied du style (en bleu dans la figure ci-dessous). Marquons chaque jour, pour un angle horaire fixe, le point de la table situé sur l'ombre portée par le gnomon, à la distance d de ce cercle, selon une progression linéaire.
Il se trouve alors que ce point décrit une courbe complexe mais dont la partie correspondant aux valeurs de l'obliquité (-23.4° à +23.4°) est très proche d'un arc de cercle.

l'arc en rouge de la courbe en gris est quasiment circulaire

 

un arc de cercle "miraculeux"

la bonne coïncidence entre courbes exactes, en vert, et arcs de cercle

Il est alors facile de tracer les lignes horaires en utilisant les deux points des solstices et celui des équinoxes.
On peut inverser le sens de la progression linéaire de la déclinaison et placer le solstice d'hiver près du centre du cadran, à la place du solstice d'été. Le cadran sera double et, suivant la saison, pour plus de précision, on lira l'heure sur les lignes rouges ou sur les lignes bleues après inversion de l'orientation.

un rapace?

un crabe?

cadran double emboîté, les deux cadrans sont séparés par les arcs des levers et couchers

Ces cadrans sont signalés par le grand spécialiste de la gnomonique italienne, l'Ammiraglio Girolamo Fantoni (1920-2006), dans son ouvrage "Orologi Solari" paru en 1988. Deux ans auparavant, en 1986, René Rohr (1905-2000), capitaine au long cours, avait fait paraître son livre "Les Cadrans Solaires".
La Gnomonique inspirerait-elle particulièrement les coureurs des mers?

Pour se servir de ces cadrans il faut une table donnant la déclinaison du soleil en fonction de la date.
L'amiral évoque une graduation en fonction du calendrier au lieu de la déclinaison. Cela peut paraître plus pratique mais on perd alors le bénéfice du miracle trigonométrique et les lignes horaires doivent être calculées et dessinées point par point.

On peut encore imaginer de faire la distinction entre les semestres suivant le signe de la déclinaison. On augmente alors sensiblement la distance entre le bord extrême de l'abaque et le pied du gnomon ce qui nuit gravement à la précision de la lecture.

deux semestres selon la valeur de la déclinaison

La variation de l'azimut en fonction de la déclinaison est brutale au moment des solstices. Sa variation en fonction du calendrier prend en compte la stagnation de la déclinaison aux environs des solstices (les bien nommés) et se trouve donc bien plus progressive.

pour les heures rondes, en bleu l'azimut en fonction de la déclinaison, en rouge en fonction du calendrier

 

deux semestres en fonction du calendrier

 Quitte à dessiner des courbes point par point, autant intégrer l'équation du temps dans les calculs.

...avec équation du temps

 Le cadran bleu dessiné ci-dessus en fonction du calendrier a été étudié par Y. Opizzo sous le nom d'araignée.

par quatre points passent trois cubiques circulaires focales

La ligne de changement de date

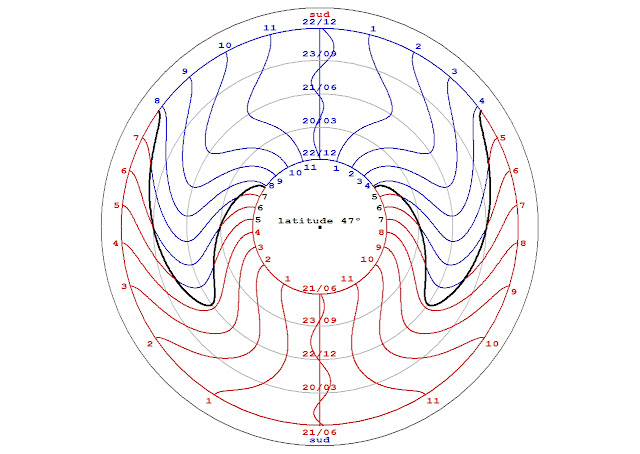
Ayent (CH)

Dans ce qui suit on parle en heure solaire, c'est à dire celle qui représente la marche du soleil en un lieu donné: par exemple, lorsque le soleil est au plus haut dans le ciel, il est midi. Et il est alors midi passé en un lieu situé un peu plus à l'est, alors qu'il n'est pas encore midi en un lieu situé un peu plus à l'ouest.
Tant que les moyens de transport restaient assez lents, chaque ville ou village avait ainsi son heure solaire, réglée par le cadran solaire.
Avec le développement des chemins de fer, il a fallu unifier, par voie administrative, les heures entre les gares. Pour fixer l'heure on a alors abandonné le soleil et déterminé une longitude de référence dont l'heure est devenue celle de tout le pays.
Dans un premier temps chaque État a choisi comme heure celle de sa capitale.
Il en est découlé des effets non négligeables dans les pays s'étendant sur une grande distance dans le sens de la longitude, c'est à dire d'est en ouest. Ainsi l'écart entre Paris et Strasbourg est égal à 5.4° ce qui représente 21.6 minutes, celui entre Brest et Paris est de 6.83° soit 27.3 minutes. Il y a ainsi un écart total de 49 minutes entre Strasbourg et Brest: ce n'est que 49 minutes après les Strasbourgeois que les Brestois voient le soleil au plus haut dans leur ciel. Leurs vies quotidiennes sont ainsi différentes quant à la lumière du jour.
Avec la vitesse croissante des moyens de transport et pour le développement des relations internationales il a fallu décider d'une référence mondiale dont dérivent alors les heures des différents États en fonction de leur écart en longitude. On a ainsi créé 24 fuseaux horaires de 15° en laissant chaque État libre de choisir le sien.
C'est le méridien de Greenwich où se trouve l'observatoire de Londres qui a été choisi en 1884 comme référence pour fixer l'heure UTC (voir article précédent intitulé 'un tour en orthodromie').
Les pays de l'Union Européenne ont presque tous choisi le fuseau +1 heure, dont le centre passe à 15° du méridien de Greenwich, un peu à l'est de Berlin et Rome et un peu à l'ouest de Vienne. L'écart entre l'est de la Pologne et l'ouest de l’Espagne atteint 37° soit 2 heures et 28 minutes!

En un lieu donné, pour passer de l'heure légale à l'heure solaire, ou inversement, il suffit de transformer en heures l'écart de longitude entre ce lieu et le centre du méridien retenu par la règlementation du pays. Ce faisant on obtient une heure solaire qualifiée de moyenne car elle ne tient pas compte de "l'équation du temps", ce qui est sans importance dans le cadre de cet article (voir l'article intitulé 'l'équation du temps' en date du 06/06/2014). En été il faut tenir compte d'un changement de fuseau horaire supplémentaire.

cadran solaire imaginé par la NASA à l'usage des astronautes de la Station Spatiale...

Les planisphères dessinés ci-dessous sont tracés suivant la projection de Mercator et ils mentionnent les heures solaires de certaines villes (voir article intitulé 'de la boussole au logarithme: la loxodromie' daté 29/03/2016).

Sur le globe terrestre il y a presque en permanence deux jours en cours. Celui en vigueur à Londres et le précédent si l'heure UTC est inférieure à 12, ou le suivant sinon. Les frontières entre les deux sont les traces du demi-méridien de minuit et du demi méridien qui passe par les antipodes de Londres. Le premier se trouve à l'opposé du soleil et tourne donc comme la terre autour du soleil pendant que la rotation diurne de la terre fait défiler dessous, quotidiennement, le second avec les continents.
En un lieu donné la date change donc chaque jour lorsque son méridien coïncide avec le méridien de minuit qui vu depuis ce lieu se déplace de l'est à l'ouest.

Ce n'est que lorsqu'il est 12 h UTC que la date est unifiée sur toute la terre, les frontières entre les deux jours coïncidant alors. Juste à cet instant, le jour précédent disparait et immédiatement nait le jour nouveau. A ce moment Londres est à l'opposé du méridien de minuit qui se trouve donc à la longitude +180° ou, ce qui revient au même, -180°.
La trace sur la terre du méridien de minuit à cet instant est donc appelée "Ligne de changement de date".
Dans les figures ci-dessous la Ligne de changement de date est dessinée en bleu et le méridien de minuit en en rouge.

2 septembre 11h00 UTC: entre les longitudes +165° et +180° on en est encore au 1er septembre

 

2 septembre 12h UTC: toute la terre est à la même date, les deux méridiens coincident

2 septembre 13h00 UTC: le 3 septembre a commencé pour les longitudes entre -180° et -165°

Ci-dessous la fabrique quotidienne des jours à 12h UTC, à l'opposé du soleil:

le 02/09 à 9h UTC: le jour 01/09, dessiné en rouge, n'a plus que 3 heures à vivre

le 02/09 12h UTC toute la terre est au jour 02/09, dessiné en vert: le nouveau jour va naître

le 02/09 à 15h UTC: le jour 02/09, en vert, abandonne du terrain au nouveau jour 03/09, en rouge

le 03/09 à 0h UTC: la terre est exactement partagée entre les jours 02/09 et 03/09

le 03/09 à 9h UTC: le jour 02/09, dessiné en vert, n'a plus que 3 heures à vivre...etc

La naissance du nouveau jour induit de sérieux inconvénients pour les habitants des zones proches de cette Ligne. En effet, la Ligne de changement de date emporte avec elle, dans la nouvelle date, les lieux situés dans les longitudes négatives mais laisse sur place, dans l'ancienne date, ceux des longitudes positives. Ainsi quand il sera midi le 3 septembre à Wellington (Nouvelle Zélande) il sera 14h22 le 2 septembre, la veille, à Papeete à 4.300 km de là.
Le problème s'aggrave pour les terres émergées qui se répartissent de part et d'autre de la Ligne comme les îles Fidji: un habitant de l'île Taveuni, par exemple, peut parfaitement, à tout moment, en chevauchant la Ligne, avoir un pied dans un jour et l'autre dans la veille!

copyright S. Lacabanne

Des aménagements règlementaires pallient ces inconvénients et, par chance (?), il existe peu de terres émergées sur la Ligne car elle passe en plein océan Pacifique.

 Les aménagements d'heure légale règlent les problèmes statiques mais pas ceux des navigateurs qui sont amenés à traverser la Ligne.
Les explorateurs espagnols Magellan (1480-1521) et Elcano (1476-1526) en firent l'expérience lors du premier tour du monde vers l'ouest, d'août 1519 à septembre 1522. Pour Elcano le jour du retour était le 5 septembre alors qu'à terre la date était le 6...
Ce premier tour du monde fut tragique: sur 237 marins embarqués seuls 18 revinrent en Espagne après une traversée complète.

Oh ! combien de marins, combien de capitaines

Qui sont partis joyeux pour des courses lointaines,

Dans ce morne horizon se sont évanouis...

Sous l'aveugle océan à jamais enfouis!

Et Philéas Fogg (!) doit à la Ligne d'avoir gagné son pari de faire le tour du monde vers l'est en 80 jours alors qu'il pensait l'avoir perdu en arrivant, selon lui, le 81ème jour...

itinéraire de Philéas Fogg décrit par Jules Verne (avec de belles orthodromies!)

Franchir la Ligne de nos jours, lors de voyages aériens, réserve des surprises.

Embarquons sur le vol qui décolle vers l'ouest de Los Angeles le 25 décembre à 22h heure locale pour Darwin en Australie.

le 25 décembre à 22h locale, soit 5h54 UTC le 26 décembre, décollage de Los Angeles vers l'ouest

Après deux heures de vol, l'heure locale est 22h51 le 25 décembre: à Los Angeles le 26 décembre commence

10h24 UTC le 26 décembre, le méridien de minuit rattrape l'avion: il est 0h le 26 décembre heure locale

le 26 décembre à 11h59 UTC: toute la terre va être à la même heure et le 27 décembre va naître

26 décembre 12h1 UTC: le 27 décembre commence aux antipodes du méridien de Greenwich

le 26 décembre 13h45 UTC, instant crucial: l'avion va franchir la Ligne, à bord il est 1h45 heure locale le 26 décembre

l'avion a franchi la Ligne: l'heure locale à bord est toujours 1h45 heure locale mais c'est le 27 décembre

l'avion survole Bikini, il est 0h43 à Darwin le 27 décembre et 8h6 à Los Angeles mais le 26 décembre

21h46 UTC le 26 décembre: l'avion atterrit à Darwin où il est 6h29 le 27 décembre

A Darwin la journée du 27 décembre se terminera à 15h17 UTC. Le bilan de l'opération pour le voyageur parti le 25 à 22h et arrivé le 27 à 6h29 est donc un 25 décembre rallongé de 2h et 30m, un 26 décembre réduit à 3h et 21m et un 27 décembre rallongé de 1h et 32m, ce qui au total donne un jour manquant et un décalage horaire de 7h et 23m.
On remarque que si l'avion avait décollé de Los Angeles à 20h15 plutôt qu'à 22h, il aurait été rattrapé par le méridien de minuit exactement sur la Ligne. Le 25 décembre aurait alors été rallongé de 4h et 6m, le 26 décembre n'aurait pas existé du tout et le 27 aurait été rallongé de 3h et 17m.
On peut compter sur les commandants de bord pour jouer sur le rallongement du 25 de façon à faire coïncider, lors des annonces en cabine aux passagers insomniaques, le passage de la Ligne et le minuit local. L'effet est garanti!

Autres surprises lors d'un voyage dans le sens inverse!

Embarquons sur le vol qui décolle vers l'est de Tokyo le 26 décembre à 6h00 heure locale pour Papeete en Polynésie française.

26 décembre 6h locale, soit 20h40 UTC même jour: décollage vers l'est

 

26 décembre 9h52 UTC, l'avion va franchir la Ligne, l'heure locale est 14h51

la Ligne est franchie, l'heure locale reste 14h51 mais fait un saut en arrière de 24h: l'avion se trouve le 25 décembre!

arrivée à Papeete le 25 décembre à 22h33, soit 8h32 UTC le 26 décembre

Ainsi, partis le 26 décembre de Tokyo à 6h, les passagers arrivent à Papeete le 25 décembre à 22h33: le voyage a duré 11h et 52m et cependant ils arrivent 7h et 27m avant d'être partis!  L'explication réside dans le rallongement de la journée du 26 qui, pour les passagers, dure 43h et 19m.
En effet au moment du décollage la journée du 26 compte déjà 6h, le voyage dure 11h et 52m et il faut attendre 1h et 27m à Papeete pour que la journée du 25 se termine: total 19h et 19m (c'est le décalage horaire entre les deux villes), ensuite une nouvelle journée entière du 26 va s'écouler. 
Pendant cette extraordinaire journée du 26 ils auront passé 7h et 6m à la date du 25!

Le nouveau calendrier ci-dessous va-t-il permettre d'y voir plus clair?

Un tour en orthodromie

loxodromie:  va en oblique

orthodromie: va tout droit

En géométrie sphérique la droite est un grand cercle: c'est le plus court chemin d'un point à un autre, ce que n'est pas la loxodromie.
Pour dessiner un planisphère, la projection de Mercator (1512-1594) reste une bonne solution, assez facile à mettre en œuvre, mais avec l'inconvénient que les hautes latitudes sont fortement dilatées.
Les loxodromies sont des droites et les grands cercles des courbes très proches de la sinusoïde et que l'on peut construire par points.
L'un de ces grands cercles est le terminateur qui sépare sur la terre le jour de la nuit.
Sa représentation chez Mercator varie suivant la saison puisqu'elle connait son maximum d'aplatissement aux solstices alors qu'aux équinoxes elle est réduite à deux segments verticaux. Cette ligne de partage est dessinée en rouge dans les figures suivantes.

au début de l'hiver la durée de la nuit dépasse celle du jour pour l'hémisphère nord

au voisinage de l'équinoxe il y a une quasi égalité

 

à la fin du printemps les durées sont inversées

 
Au temps de Mercator, le méridien origine était celui du lieu où coïncidaient nord magnétique et nord géographique: au Cap Verd. Le roi Louis XIII, en 1634, avait imposé comme méridien origine celui qui passe à 20° à l'ouest de Paris à l'île de Fer aux Canaries.
La conférence de Washington d'octobre 1884, a décidé, en raison de la suprématie maritime britannique et au grand dam de la France, que le méridien de référence pour l'heure universelle serait celui de Greenwich où se trouve l'observatoire de Londres. En échange de la capitulation française, le Royaume Uni devait se rallier au système métrique mis au point par les savants français en 1799, promesse que la perfide Albion n'a pas tenue...
L'heure GMT (Greenwich Mean Time) et le temps universel (TU) ont cédé la place en 1988 au temps UTC (Temps universel coordonné).

loxodromies, orthodromies, heures solaires mondiales

 Pour quelques destinations est indiquée sur la figure l'heure solaire locale.
Les dessins des grands cercles ressemblent à celui du terminateur. Ils sont plus ou moins dilatés suivant l'importance de la différence de latitude entre l'origine et la destination. Contrairement à ce qu'on lit sur la figure ces arcs de grand cercle représentent des trajets plus courts que les segments de loxodromie!

Le planisphère montre que pour aller de Londres à Wellington (Nouvelle Zélande) il vaut mieux passer par Tokyo. Par contre pour revenir en Europe les itinéraires les plus économiques seront différents si la destination est Rome ou Madrid: pour Rome mieux vaut passer par Singapour alors que pour Madrid il vaut mieux survoler Kampala en Ouganda. Tout cela, bien sûr, sans tenir compte de considérations géopolitiques.
Pour Papeete le mieux est de survoler Los Angeles.

De Londres à New York la différence de distance entre loxodromie (segment en bleu) et orthodromie (arc en vert) atteint 230 km. Cela représente 4% de la distance totale. Au temps du ruban bleu les navires pouvaient donc gagner 4 heures sur les 100 h du voyage. Mais, et c'est la rançon du gain de temps, il faut passer plus au nord que la loxodromie.
Lors de la première traversée du Titanic, en avril 1912, le commandant Edward Smith (1850-1912) a suivi une route qui passe plus au sud, même, que la loxodromie, de façon à éviter les nombreux icebergs qui, ce printemps là, descendaient anormalement vers le sud. Ni lui, ni la White Star Line ne peuvent être taxés d'avoir voulu à tout prix gagner le ruban bleu à la première traversée. L'hiver 1911-1912 avait été particulièrement long et rigoureux en Amérique du Nord et cette vague de froid exceptionnelle pourrait avoir sa part dans l'explication du naufrage du 14 avril 1912 qui fit 1500 noyés (le lieu du naufrage est dessiné sur le planisphère ci dessus).

La géométrie sphérique règlemente l'orthodromie.
La distance angulaire entre deux points de coordonnées (lon1, lat1) et (lon2, lat2) est donnée par la formule classique:
cos(distance) = sin(lat1)sin(lat2)+cos(lat1)cos(lat2)cos(lon2-lon1)
Le cap à suivre au départ, cap0,  est donné par:
tan(cap0) = sin(lon2-lon1)/(tan(lat2)cos(lat1)-sin(lat1)cos(lon2-lon1))
et aussi par: sin(cap0) = cos(lat2)sin(lon2-lon1)/sin(distance)
Il en découle que pour toute destination se trouvant dans l'hémisphère défini par le plan passant par le point de départ et perpendiculaire au méridien du lieu, et par le pôle nord (pour un départ depuis l'hémisphère nord) la direction de départ est tournée vers le nord. Pour tout point du grand cercle intersection de la sphère et du plan ci-dessus, et notamment pour les antipodes, le cap de départ vaut 90°.

en bleu la loxodromie, en vert l'orthodromie

La caractéristique essentielle d'une orthodromie est le vertex c'est à dire le point de plus forte latitude de l'itinéraire. Les coordonnées de ce point, lonV et latV, sont données par:
tan(lonV-lon1) =  1/(tan(cap0)sin(lat1))
cos(latV) = cos(lat1)sin(cap0)
L'équation du grand cercle est, lonA et latA étant les coordonnées du point courant:
tan(latA) = tan(latV).cos(lonA-lonV).
Le cap à suivre au point A est donné par capA = pi - arcsin(cos(latV)/cos(latA)).
On a la relation: sin(capA).cos(latA) = cos(latV) = constante.
Il en résulte qu'en tout point de l'itinéraire, si l'on connait la latitude, le cap à suivre s'en déduit automatiquement.

Avant la mise au point du pilote automatique on a pratiqué la navigation à l'estime. Le terme 'estime' n'a ici rien à voir avec la pratique de la vue de nez ou du doigt mouillé, quoi qu'en disent trop d'auteurs! La technique de l'estime a des bases mathématiques.
Elle permet de calculer une approximation d'une position à partir de la précédente et de la connaissance du chemin parcouru S et de l'angle de route R.
On a recours à l'équation de la loxodromie qui s'écrit: lon2 - lon1 = (lac2 -lac1).tan(R) où lac est la latitude croissante (voir article du mois précédent intitulé 'de la boussole au logarithme: la loxodromie').
L'approximation consiste à remplacer le facteur (lac2 - lac1) par sa dérivée. En appelant lam la moyenne de lat1 et lat2 cette dérivée s'écrit (lat2-lat1)/cos(lam).
Pour la latitude on retient l’approximation: lat2 - lat1 =  S.cos(R).
On obtient alors: lon2 = lon1 + S.sin(R)/cos(lam).
Ce sont là les formules de la navigation à l'estime, valables tant que le chemin parcouru reste faible.
Elles semblent avoir été utilisées de façon empirique dès le moyen âge.

Les cartes utilisables en mer sont des projections de Mercator sur lesquelles ne peuvent figurer les orthodromies.
L’Ingénieur Général Hydrographe de la Marine Alexandre-Pierre Givry (1785-1867) a mis au point une technique pour tracer facilement sur une carte de Mercator une orthodromie approchée, joignant deux points pas trop espacés.
Givry assimile l'arc d’orthodromie dessiné sur la carte Mercator à un arc de cercle. En développant la formule des sinus qui veut que le rapport des sinus des angles de route orthodromique au départ et à l'arrivée soit égal à l'inverse du rapport des cosinus des latitudes, on peut, à l'issue d'une cuisine trigonométrique très 19ème siècle, éliminer ces angles de route.
En appelant C la correction Givry, c'est à dire l'angle à ajouter à la route loxodromique désignée par R, on obtient avec les mêmes notations que ci-dessus, l'égalité suivante:
tan(C) = tan(R).tan((lat2-lat1)/2).tan(lam).
On élimine alors R par la formule de la navigation à l'estime: tan(R) = ((lon2-lon1)/(lat2-lat1)).cos(lam).
Et en faisant l'hypothèse que la différence de latitude reste faible (angle égal à sa tangente), on obtient:
tan(C) = (1/2)(lon2-lon1).sin(lam).

Le résultat est remarquable de simplicité... et d'approximation comme le montre la figure ci-dessous:

en noir l'arc de cercle Givry, en vert l'orthodromie

 Embarquons sur le jet, dessiné en bleu dans les figures ci-dessous, qui part le 25 décembre à 14h de Londres pour Darwin (130.8 E, 12.4 S) en Australie, sans escale (!).

décollage à 14h00 UTC

Au moment du départ il est 22h43 à Darwin et c'est la nuit la plus courte de l'année.
Le vol durera un peu plus de 17h. La distance orthodromique est de 13.850 km et elle permet d'économiser une heure de vol (770 km) sur la distance loxodromique.
La latitude du vertex est de 56.1°, soit 4.6° plus au nord que Londres, le cap de départ sera 63.8° (nord nord-est) et tout au long du voyage on aura l’identité sin(cap).cos(lat) = 0.558.
Il restera au pilote à tenir compte de la dérive due aux vents...

à 14h55 UTC le soleil se couche sur l'avion après 0h55 de vol, à Londres ce sera à 15h48, presqu'une heure plus tard.

 L'avion gagne en latitude et atteint le vertex à la latitude de 56.1° après 2h42 de vol.
La longitude de ce point est de 32.3°E, l'avion passera donc la ligne de l'équateur à la longitude 90 + 32.3 = 122.3°E. A ce moment, en vertu du lien entre cap et latitude, le cap sera égal à la latitude du vertex augmentée de 90°: 146.1°.
Moscou est survolé à 17h07 UTC: il est au sol 19h37.

19h35 UTC l'avion rencontre le méridien de changement de date locale

L'avion retrouve la latitude de Londres aux environs d'Astana capitale du Kazakhstan et minuit arrive avec 4h25 d'avance, autant de temps perdu pour les passagers!

0h15 UTC le soleil se lève sur l'avion, la nuit a duré 9h20, la précédente à Londres avait duré 16h20, il est 6h56 au sol

Après le survol de Hanoï l'avion passera la ligne de l'équateur, à la longitude 122.3°, au dessus de Bornéo, à 5h14 UTC, il sera 13h23 au sol.

atterrissage à 16h02 locales, il est 7h19 à Londres

L'avion parti le 25/12 à 14h, arrive le 26/12 à 16h02 après 17h19 de vol.
Pendant le vol qui a duré 17h19 les passagers ont vécu administrativement 26h02. L'excédent de 8h43 est égal au décalage horaire entre Londres et Darwin.
Le soleil se couchera à Darwin à 18h24, soit 9h39 UTC, c'est à dire une heure et demi après qu'il se soit levé à Londres: nuit et jour sont inversés...

créationnisme et darwinisme