le cadran solaire azimutal à gnomon fixe

florilège de cubiques circulaires focales partageant foyer et asymptote

Il s'agit dans cet article de la mise en œuvre d'une quatrième coïncidence trigonométrique!

Un premier "miracle" a permis de construire le quadrant universel, basé sur la hauteur du soleil, dont les lignes des heures inégales sont faciles à tracer car il s'agit à très peu de choses près d'arcs de cercle (voir à ce sujet l'article du présent blog en date du 17-10-2014 intitulé "La magie du quadrant d'heures inégales"). Cet objet individuel, sorte de montre de l'Antiquité et du Moyen Age, devait être assez répandu ainsi que ses variantes: quadrant d'heures égales, quadrant du tableau des ambassadeurs...etc (voir à ce sujet l'article du présent blog en date du 19/11/2014 intitulé "les cadrans de hauteur à style").

Un second "miracle" a conféré une grande simplicité d’exécution aux cadrans de l'Antiquité, à gnomon perpendiculaire, car les lignes des heures inégales sont alors à très peu de choses près des segments de droite. Il s'agit là de cadrans fixes, car il faut les orienter exactement, et souvent monumentaux. Tel le cadran horizontal d'Auguste au Champ de Mars à Rome ou ceux, verticaux, de la Tour des Vents à Athènes. Pour ces cadrans c'est l’extrémité du gnomon qui désigne l'heure sur un abaque tracé sur la table.
Le traité de Ptolémée, "L'Analemme", donne la méthode utile au dessin de ces abaques (voir à ce sujet l'article du présent blog en date du 12-11-2015 intitulé "Le Traité de l'Analemme, par Ptolémée").

Bien plus tardivement on imaginera de remplacer le gnomon perpendiculaire par un style pointé vers le pôle nord et donc incliné sur la table du cadran. On constatera alors que les lignes des heures classiques sont les droites que forme l'ombre de l'axe du monde matérialisé par le style. Mais il ne s'agira plus alors de "miracle" parce que cela résulte de la simple trigonométrie.

Un troisième "miracle" a encore présidé à la mise au point de l'anneau de paysan et de ses dérivés tels la bague solaire... 

La coïncidence qui nous occupe ici concerne un cadran d'heures classiques basé non plus sur la hauteur du soleil mais sur son autre coordonnée locale: son azimut.
A la différence des autres cadrans d'azimut (cadran analemmatique, cadran d'Oughtred, cadran orthographique) qui résultent d'une projection, l'abaque de celui-ci est fait de cercles concentriques autour du pied du gnomon.
L'azimut A est donné par la formule tanA = sinH / (cosH.sinl - tand.cosl) où H est l'angle horaire, l la latitude et d la déclinaison.
Traçons un cercle de référence, de rayon quelconque, centré sur le pied du style (en bleu dans la figure ci-dessous). Marquons chaque jour, pour un angle horaire fixe, le point de la table situé sur l'ombre portée par le gnomon, à la distance d de ce cercle, selon une progression linéaire.
Il se trouve alors que ce point décrit une courbe complexe mais dont la partie correspondant aux valeurs de l'obliquité (-23.4° à +23.4°) est très proche d'un arc de cercle.

l'arc en rouge de la courbe en gris est quasiment circulaire

 

un arc de cercle "miraculeux"

la bonne coïncidence entre courbes exactes, en vert, et arcs de cercle

Il est alors facile de tracer les lignes horaires en utilisant les deux points des solstices et celui des équinoxes.
On peut inverser le sens de la progression linéaire de la déclinaison et placer le solstice d'hiver près du centre du cadran, à la place du solstice d'été. Le cadran sera double et, suivant la saison, pour plus de précision, on lira l'heure sur les lignes rouges ou sur les lignes bleues après inversion de l'orientation.

un rapace?

un crabe?

cadran double emboîté, les deux cadrans sont séparés par les arcs des levers et couchers

Ces cadrans sont signalés par le grand spécialiste de la gnomonique italienne, l'Ammiraglio Girolamo Fantoni (1920-2006), dans son ouvrage "Orologi Solari" paru en 1988. Deux ans auparavant, en 1986, René Rohr (1905-2000), capitaine au long cours, avait fait paraître son livre "Les Cadrans Solaires".
La Gnomonique inspirerait-elle particulièrement les coureurs des mers?

Pour se servir de ces cadrans il faut une table donnant la déclinaison du soleil en fonction de la date.
L'amiral évoque une graduation en fonction du calendrier au lieu de la déclinaison. Cela peut paraître plus pratique mais on perd alors le bénéfice du miracle trigonométrique et les lignes horaires doivent être calculées et dessinées point par point.

On peut encore imaginer de faire la distinction entre les semestres suivant le signe de la déclinaison. On augmente alors sensiblement la distance entre le bord extrême de l'abaque et le pied du gnomon ce qui nuit gravement à la précision de la lecture.

deux semestres selon la valeur de la déclinaison

La variation de l'azimut en fonction de la déclinaison est brutale au moment des solstices. Sa variation en fonction du calendrier prend en compte la stagnation de la déclinaison aux environs des solstices (les bien nommés) et se trouve donc bien plus progressive.

pour les heures rondes, en bleu l'azimut en fonction de la déclinaison, en rouge en fonction du calendrier

 

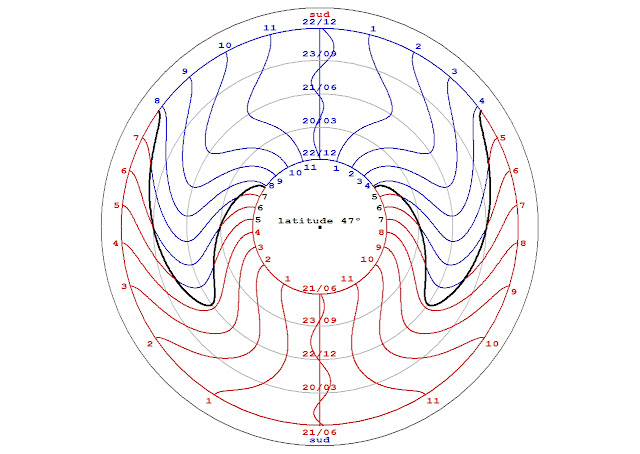deux semestres en fonction du calendrier

 Quitte à dessiner des courbes point par point, autant intégrer l'équation du temps dans les calculs.

...avec équation du temps

 Le cadran bleu dessiné ci-dessus en fonction du calendrier a été étudié par Y. Opizzo sous le nom d'araignée.

par quatre points passent trois cubiques circulaires focales