Le cadran solaire méridional bifilaire à lignes horaires équi-angulaires

 

Michnik 1922

 En 1922 le mathématicien allemand Hugo Michnik découvre et étudie un cadran solaire dont le style polaire est remplacé par deux fils perpendiculaires entre eux et placés parallèlement au plan du cadran.

Cette découverte extraordinaire et insoupçonnable ouvre un champ d'études nouveau aux gnomonistes: on pourrait parler de "miracle de Michnik" comme on parle du "miracle de Morley" en l'honneur du mathématicien anglais Frank Morley (1860/1937) qui a découvert en 1898 que les trisectrices d'un triangle quelconque se coupent en formant un triangle équilatéral.

le "miracle de Morley" 1898

 

Les spécialistes ont porté cette invention jusqu'au cadran muni de deux fils quelconques projetant leurs ombres sur une table sans orientation particulière. Il en découle des lignes horaires relevant plus de l'art graphique que de la quête de l'heure.

Les écrits de Dominique Collin consultables sur internet sont fondateurs en matière de cadrans bifilaires.

L'intérêt principal du miracle de Michnik réside dans la simplicité et l'élégance des lignes horaires.

On s'intéresse ici au cadran méridional

 

Les fils, l'un dans le sens est/ouest, l'autre vertical, sont placés à des distances différentes et constituent chacun la ligne décrite, au cours de la journée, par le sommet d'un style mobile non matérialisé. L'intersection des lignes d'ombre projetées, l'une horizontale, l'autre verticale donne un point d'ombre qui indique l'heure sur un abaque adéquat.

Soit la la latitude du lieu, a la distance au cadran du fil vertical et b celle du fil horizontal.

Avec un axe des abscisses oy horizontal vers l’est et un axe des ordonnées oz vertical vers le bas, les formules horaires classiques donnent l'équation de la ligne d'ombre pour chacun des deux fils, et donc les coordonnées du point d'ombre P:

y = a*sin(H)/(sin(la)cos(H)-cos(la)tan(d)) et

z = b*(cos(la)cos(H)+sin(la)tan(d))/(sin(la)cos(H)-cos(la)tan(d))

où H est l'angle horaire et d la déclinaison du Soleil.

L'élimination de la déclinaison de ces coordonnées, assez simple, donne l'équation des lignes horaires tracées sur le cadran:

y*b*cos(H)+z*a*cos(la)sin(H)+a*b*sin(la)sin(H) = 0.

Ce sont des droites qui, quel que soit l'angle horaire H, coupent l'axe oz (y = 0) au point d' ordonnée -b*tan(la) qui est donc le point de concours d'où elles rayonnent.

Leur pente est proportionnelle à la tangente de l'angle horaire: (a/b)*cos(la)tan(H).

La dualité des deux styles fictifs mobiles et coordonnés que constituent les fils permet donc au gnomoniste, en jouant sur le rapport des distances des fils au cadran, de choisir la pente des lignes horaires et donc de décider de son aspect.

Pour b = a, on retrouve le cadran classique à style polaire centré au point de concours qui présente une rose horaire analogue puisque la pente des lignes horaires, cos(la)tan(H), n'en est qu'un multiple...mais les angles horaires ne coïncident pas.

L'intérêt du cadran bifilaire connait son acmé lorsque la pente de la ligne horaire est égale à tan(H) car les lignes horaires sont alors régulièrement espacées de 15°. Il faut et il suffit de choisir pour b la valeur a*cos(la).

Le cadran évoque ainsi avec élégance une demi horloge qui serait graduée en 24 heures.

Cette circonstance facilite aussi la lecture de l'heure entre deux lignes.

 

Dans la suite on s'intéresse au cadran à lignes horaires équi-angulaires pour lequel b = a*cos(la)

 

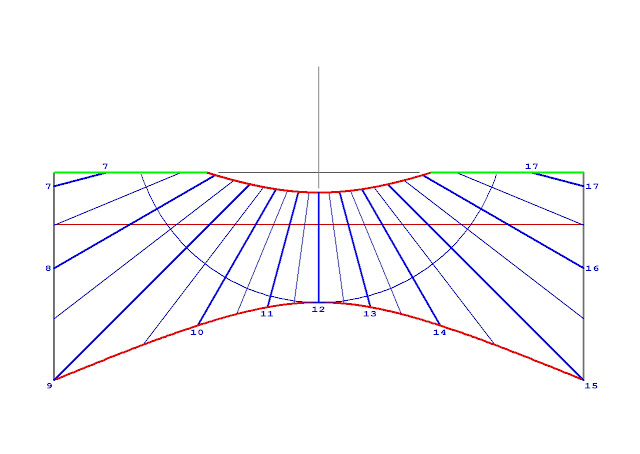latitude 47.3°

 

Pour faciliter la lecture on peut remplacer les fils par des plaques pleines et de faible épaisseur:

L'analemme permet de tenir compte de l'équation du temps

 

Les relations, en fonction de l'angle horaire et de la déclinaison, entre les points utiles des deux fils sommets des styles mobiles sont assez simples.

 

 

Les coordonnées locales du point d'ombre P, où h est la hauteur du Soleil et A son azimut, sont données par:

y = a*tan(A)            z = a*cos(la)tan(h)/cos(A)

Pour alléger les formules on utilise le paramètre W égal à tan(h)/cos(A). Ce paramètre fait le lien entre coordonnées locales et coordonnées horaires:

W = tan(h)/cos(A) = (cos(la)cos(H)+sin(la)tan(d))/(sin(la)cos(H)-cos(la)tan(d)).

On a: z = a*cos(la)*W. On peut noter que la pente de la demi droite oP est égale à cos(la)tan(h)/sin(A).

 

 

 

Soient U et V, respectivement, les points utiles des fils vertical et horizontal.

L'abscisse de la projection du point V sur l'axe oy est égale à v = (a-b)tan(A), elle est proportionnelle à l'abscisse du point d'ombre qui vaut a*tan(A): v = y*(a-b)/a soit v = y*(1-cos(la)).

L'ordonnée de la projection du point U sur l'axe oz est égale à u = (a-b)tan(h)/cos(A), elle est proportionnelle à l'ordonnée du point d'ombre qui vaut a*cos(la)*W: u = z*((a-b)/a)cos(la), soit u = z*cos(la)*(1-cos(la)).

Cette relation entre les coordonnées, y et z, du  point d'ombre et celles, v et u, des points utiles des fils vertical et horizontal ne dépend ni de l'angle horaire ni de la déclinaison.

La pente de la droite joignant les projections de U et V est égale à tan(h)/sin(A), c'est celle de la demi-droite oP affectée du diviseur cos(la).

Par ailleurs, il existe, pour toute valeur du couple hauteur h et azimut A, un point Z sur l'axe oz tel que le cadran solaire vertical classique de sommet Z et de style polaire ZU, de longueur égale à a/cos(la), donne le même point d'ombre que le bifilaire.

L'angle en C, centre du cadran bifilaire, est égal à H, celui en Z, H', est donné, par construction, par tan(H') = cos(la)tan(H). Le calcul par le théorème de Thalès montre que le point Z a pour ordonnée sur l'axe oz:

oZ = a*(W*(1-cos(la))+tan(la)).

Tout se passe comme si les points d'ombre étaient ceux du cadran "mobile" dont le sommet est implanté sur l'axe à une distance fonction de la hauteur et de l'azimut du Soleil et égale à oZ, le style polaire ayant la longueur a*/cos(la).

Le cadran bifilaire à lignes horaires équiangulaires présente donc aussi l'intérêt de diminuer sensiblement la dimension verticale de l'objet, dans le rapport du cosinus de la latitude.

 

Les arcs diurnes s'obtiennent en éliminant l'angle horaire des coordonnées du point d'ombre.

L'affaire, moins simple que pour les lignes horaires et menée à bien par Dominique Collin, montre que ces courbes sont des coniques.

Pour le tracé de ces hyperboles, une méthode géométrique est employée ici.

L'ordonnée sur la ligne de midi du centre C de l'hyperbole, se calcule en faisant H = 0, d'abord avec la valeur d de la déclinaison puis avec la valeur -d. Ce point est le centre du repère C, Cy', Cz dans lequel on va définir l'hyperbole comme courbe paramétrée.

On obtient: oC = a*sin(la)/(cos^2(d)tan^2(la)-sin^2(d)).

De la même façon, le demi axe focal, vertical, aH est égal à:

aH = a*cos(la)tan(d)/(sin^2(la)-cos^2(la)tan^2(d)).

Le demi axe non focal, bH, peut être calculé en considérant l'instant du passage du Soleil au premier vertical: le point d'ombre se trouve alors à l'infini sur l'asymptote.

La pente de la droite reliant le centre au point d'ombre est égale à cos(la)tan(h)/sin(A).

A l'instant du passage au premier vertical A = pi/2 et sin(h) = sin(d)/sin(la).

La pente de l'asymptote est donc: pH = cos(la)tan(arcsin(sin(d)/sin(la))). On en déduit bH = aH/pH.

Connaissant les deux demi axes, le tracé de l'hyperbole paramétrée en découle alors dans le repère approprié: yH = bH*tan(t) et zH = aH/cos(t).

 

heure, azimut et hauteur

 

Les courbes de hauteur sont des hyperboles dont le centre est celui du cadran. Ce sont les courbes paramétrées dérivant directement des formules donnant les coordonnées locales du point d'ombre:  y = a*tan(t) et z = a*cos(la)tan(h)/cos(t).

Une courbe de hauteur h coupe l'arc diurne du solstice d'été pour  cos(t) = (sin(h)sin(la)-sin(23.438*pi/180))/(cos(h)cos(la).

Sans surcharger le cadran, on peut utiliser les deux lignes d'ombre verticale et horizontale pour connaître l'azimut et la hauteur du Soleil.

En prolongeant, à l’œil, l'ombre verticale jusqu'à une ligne horizontale placée en bas du cadran et graduée suivant la fonction tangente, on obtient la valeur de l'azimut.

De plus, si on place cette échelle des azimuts à une distance égale à la distance a, à partir du point horaire à midi au solstice d'été par exemple, on matérialise l'angle égal à l'azimut.

En considérant alors l'arc de cercle ayant pour centre le centre du cadran et tangent à l'ombre horizontale et en menant depuis ce centre une parallèle à l'indication géométrique de l'azimut, on obtient à leur intersection un point qui, par projection sur la ligne de midi munie d'une graduation suivant la fonction tangente, donne la hauteur.

 

Michnik, un cadran simple, compact, précis, complet et beau!

 

Morley et compagnie...